Question
A particle of mass $$2\,kg$$ is on a smooth horizontal table and moves in a circular path of radius $$0.6\,m.$$ The height of the table from the ground is $$0.8\,m.$$ If the angular speed of the particle is $$12\,rad\,{s^{ - 1}},$$ the magnitude of its angular momentum about a point on the ground right under the centre of the circle is
A.
$$14.4\,kg\,{m^2}{s^{ - 1}}$$
B.
$$8.64\,kg\,{m^2}{s^{ - 1}}$$
C.
$$20.16\,kg\,{m^2}{s^{ - 1}}$$
D.
$$11.52\,kg\,{m^2}{s^{ - 1}}$$
Answer :
$$14.4\,kg\,{m^2}{s^{ - 1}}$$
Solution :
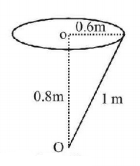
Angular momentum,
$$\eqalign{ & {L_0} = mvr\sin {90^ \circ } \cr & = 2 \times 0.6 \times 12 \times 1 \times 1\,\,\left[ {{\text{As}}\,V = r\omega ,\sin {{90}^ \circ } = 1} \right] \cr & {\text{So,}}\,\,{L_0} = 14.4\,kg{m^2}/s \cr} $$

Angular momentum,
$$\eqalign{ & {L_0} = mvr\sin {90^ \circ } \cr & = 2 \times 0.6 \times 12 \times 1 \times 1\,\,\left[ {{\text{As}}\,V = r\omega ,\sin {{90}^ \circ } = 1} \right] \cr & {\text{So,}}\,\,{L_0} = 14.4\,kg{m^2}/s \cr} $$