Question
A particle is moving eastwards with a velocity of $$5\,m{s^{ - 1}}.$$ In $$10$$ seconds the velocity changes to $$5\,m{s^{ - 1}}$$ northwards. The average acceleration in this time is-
A.
$$\frac{1}{2}\,m{s^{ - 2}}$$ towards north
B.
$$\frac{1}{{\sqrt 2 }}\,m{s^{ - 2}}$$ towards north-east
C.
$$\frac{1}{{\sqrt 2 }}\,m{s^{ - 2}}$$ towards north-west
D.
Zero
Answer :
$$\frac{1}{{\sqrt 2 }}\,m{s^{ - 2}}$$ towards north-west
Solution :
$${\text{Average acceleration}} = \frac{{{\text{change in velocity}}}}{{{\text{time interval}}}}$$
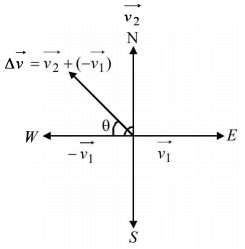
$$\eqalign{ & = \frac{{\Delta \overrightarrow v }}{t} \cr & \overrightarrow {{v_1}} = 5\hat i,\,\,\overrightarrow {{v_2}} = 5\hat j \cr & \therefore \overrightarrow a = \frac{{5\hat j - 5\hat i}}{{10}} = \frac{{\hat j - \hat i}}{2} \cr & \therefore a = \frac{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }}{2} = \frac{{\sqrt 2 }}{2} = \frac{1}{{\sqrt 2 }}\,m{s^{ - 2}} \cr & \tan \theta = \frac{{{v_2}}}{{{v_1}}} = \frac{5}{5} = 1 \cr & \therefore \theta = {45^ \circ } \cr} $$
Therefore the direction is North-west.
$${\text{Average acceleration}} = \frac{{{\text{change in velocity}}}}{{{\text{time interval}}}}$$

$$\eqalign{ & = \frac{{\Delta \overrightarrow v }}{t} \cr & \overrightarrow {{v_1}} = 5\hat i,\,\,\overrightarrow {{v_2}} = 5\hat j \cr & \therefore \overrightarrow a = \frac{{5\hat j - 5\hat i}}{{10}} = \frac{{\hat j - \hat i}}{2} \cr & \therefore a = \frac{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }}{2} = \frac{{\sqrt 2 }}{2} = \frac{1}{{\sqrt 2 }}\,m{s^{ - 2}} \cr & \tan \theta = \frac{{{v_2}}}{{{v_1}}} = \frac{5}{5} = 1 \cr & \therefore \theta = {45^ \circ } \cr} $$
Therefore the direction is North-west.