Question
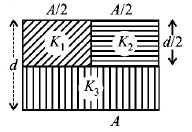
A parallel plate capacitor of area $$A,$$ plate separation $$d$$ and capacitance $$C$$ is filled with three different dielectric materials having dielectric constants $${k_1},{k_2}$$ and $${k_3}$$ as shown. If a single dielectric material is to be used to have the same capacitance $$C$$ in this capacitor, then its dielectric constant $$k$$ is given by
A parallel plate capacitor of area $$A,$$ plate separation $$d$$ and capacitance $$C$$ is filled with three different dielectric materials having dielectric constants $${k_1},{k_2}$$ and $${k_3}$$ as shown. If a single dielectric material is to be used to have the same capacitance $$C$$ in this capacitor, then its dielectric constant $$k$$ is given by
A.
$$\frac{1}{K} = \frac{1}{{{K_1}}} + \frac{1}{{{K_2}}} + \frac{1}{{2{K_3}}}$$
B.
$$\frac{1}{K} = \frac{1}{{{K_1} + {K_2}}} + \frac{1}{{2{K_3}}}$$
C.
$$K = \frac{{{K_1}{K_2}}}{{{K_1} + {K_2}}} + 2{K_3}$$
D.
$$K = {K_1} + {K_2} + 2{K_3}$$
Answer :
$$\frac{1}{K} = \frac{1}{{{K_1} + {K_2}}} + \frac{1}{{2{K_3}}}$$
Solution :
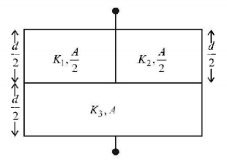
Let $${C_1} =$$ Capacity of capacitor with $${K_1}$$
$${C_2} =$$ Capacity of capacitor with $${K_2}$$
$${C_3} =$$ Capacity of capacitor with $${K_3}$$
$$\eqalign{ & \therefore {C_1} = {K_1}\left( {\frac{A}{2}} \right)\frac{{{\varepsilon _0} \times 2}}{d} = \frac{{A{\varepsilon _0}{K_1}}}{d} \cr & \therefore {C_2} = {K_2}\left( {\frac{A}{2}} \right)\frac{{{\varepsilon _0} \times 2}}{d} = \frac{{A{\varepsilon _0}{K_2}}}{d} \cr & \therefore {C_3} = {K_3}\left( A \right)\frac{{{\varepsilon _0} \times 2}}{d} = \frac{{2A{\varepsilon _0}{K_3}}}{d} \cr} $$
$${C_1}$$ and $${C_2}$$ are in parallel
$$\therefore {C_{eq}} = \frac{{A{\varepsilon _0}}}{d}\left( {{K_1} + {K_2}} \right)$$
$${C_{eq}}$$ and $${C_3}$$ are in series
$$\therefore \quad \frac{1}{C} = \frac{d}{{A{\varepsilon _0}\left( {{K_1} + {K_2}} \right)}} + \frac{d}{{2A{\varepsilon _0}{K_3}}}$$
But $$C = \frac{{KA{\varepsilon _0}}}{d}$$ for single equivalent capacitor
$$\eqalign{ & \therefore \frac{d}{{KA{\varepsilon _0}}} = \frac{d}{{A{\varepsilon _0}\left( {{K_1} + {K_2}} \right)}} + \frac{d}{{2A{\varepsilon _0}{K_3}}} \cr & {\text{or}}\,\frac{1}{K} = \frac{1}{{{K_1} + {K_2}}} + \frac{1}{{2{K_3}}} \cr} $$

Let $${C_1} =$$ Capacity of capacitor with $${K_1}$$
$${C_2} =$$ Capacity of capacitor with $${K_2}$$
$${C_3} =$$ Capacity of capacitor with $${K_3}$$
$$\eqalign{ & \therefore {C_1} = {K_1}\left( {\frac{A}{2}} \right)\frac{{{\varepsilon _0} \times 2}}{d} = \frac{{A{\varepsilon _0}{K_1}}}{d} \cr & \therefore {C_2} = {K_2}\left( {\frac{A}{2}} \right)\frac{{{\varepsilon _0} \times 2}}{d} = \frac{{A{\varepsilon _0}{K_2}}}{d} \cr & \therefore {C_3} = {K_3}\left( A \right)\frac{{{\varepsilon _0} \times 2}}{d} = \frac{{2A{\varepsilon _0}{K_3}}}{d} \cr} $$
$${C_1}$$ and $${C_2}$$ are in parallel
$$\therefore {C_{eq}} = \frac{{A{\varepsilon _0}}}{d}\left( {{K_1} + {K_2}} \right)$$
$${C_{eq}}$$ and $${C_3}$$ are in series
$$\therefore \quad \frac{1}{C} = \frac{d}{{A{\varepsilon _0}\left( {{K_1} + {K_2}} \right)}} + \frac{d}{{2A{\varepsilon _0}{K_3}}}$$
But $$C = \frac{{KA{\varepsilon _0}}}{d}$$ for single equivalent capacitor
$$\eqalign{ & \therefore \frac{d}{{KA{\varepsilon _0}}} = \frac{d}{{A{\varepsilon _0}\left( {{K_1} + {K_2}} \right)}} + \frac{d}{{2A{\varepsilon _0}{K_3}}} \cr & {\text{or}}\,\frac{1}{K} = \frac{1}{{{K_1} + {K_2}}} + \frac{1}{{2{K_3}}} \cr} $$