Question
A parallel beam of light $$\left( {\lambda = 5000\,\mathop {\text{A}}\limits^ \circ } \right)$$ is incident at an angle $$\alpha = {30^ \circ }$$ with the normal to the slit plane in $$YDSE.$$ Assume that the intensity due to each slit at any point on the screen is $${I_0}.$$ Point $$O$$ is equidistant from $${S_1}$$ and $${S_2}.$$ The distance between slit is $$1\,mm,$$ then the intensity at
A parallel beam of light $$\left( {\lambda = 5000\,\mathop {\text{A}}\limits^ \circ } \right)$$ is incident at an angle $$\alpha = {30^ \circ }$$ with the normal to the slit plane in $$YDSE.$$ Assume that the intensity due to each slit at any point on the screen is $${I_0}.$$ Point $$O$$ is equidistant from $${S_1}$$ and $${S_2}.$$ The distance between slit is $$1\,mm,$$ then the intensity at
A.
$$O$$ is $$3\,{I_0}$$
B.
$$O$$ is zero
C.
a point $$1\,m$$ below $$O$$ is $$4\,{I_0}$$
D.
a point in the screen $$1\,m$$ below $$O$$ is zero
Answer :
a point $$1\,m$$ below $$O$$ is $$4\,{I_0}$$
Solution :
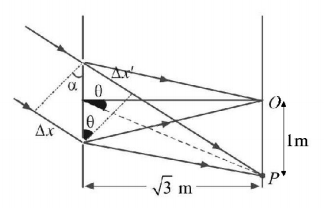
The path difference at $$O,$$
$$\eqalign{ & \Delta x = d\sin \alpha = d\sin {30^ \circ } = \frac{{{{10}^{ - 3}}}}{2}m \cr & {\text{Now,}}\,\phi = \frac{{2\pi }}{\lambda }.\Delta x = \frac{{2\pi }}{{5000 \times {{10}^{ - 10}}}} \times \frac{{{{10}^{ - 3}}}}{2} = 2\pi \times {10^3} \cr & {\text{So}}\,I = {I_0} + {I_0} + 2\sqrt {{I_0}{I_0}} \cos \left( {2\pi \times {{10}^3}} \right) = 4{I_0} \cr} $$
The angular position of $$P,\tan \theta = \frac{1}{{\sqrt 3 }};$$ or $$\theta = {30^ \circ }.$$ It means path difference at $$P$$ is also $$\Delta x$$ and hence $$I = 4{I_0}$$

The path difference at $$O,$$
$$\eqalign{ & \Delta x = d\sin \alpha = d\sin {30^ \circ } = \frac{{{{10}^{ - 3}}}}{2}m \cr & {\text{Now,}}\,\phi = \frac{{2\pi }}{\lambda }.\Delta x = \frac{{2\pi }}{{5000 \times {{10}^{ - 10}}}} \times \frac{{{{10}^{ - 3}}}}{2} = 2\pi \times {10^3} \cr & {\text{So}}\,I = {I_0} + {I_0} + 2\sqrt {{I_0}{I_0}} \cos \left( {2\pi \times {{10}^3}} \right) = 4{I_0} \cr} $$
The angular position of $$P,\tan \theta = \frac{1}{{\sqrt 3 }};$$ or $$\theta = {30^ \circ }.$$ It means path difference at $$P$$ is also $$\Delta x$$ and hence $$I = 4{I_0}$$