Question
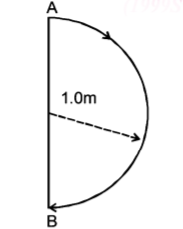
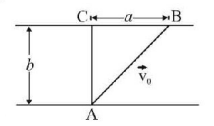
A man in a row boat must get from point $$A$$ to point $$B$$ on the opposite bank of the river (see figure). The distance $$BC = a.$$ The width of the river $$AC = b.$$ At what minimum speed $$u$$ relative to the still water should the boat travel to reach the point $$B?$$ The velocity of flow of the river is $${v_0}.$$
A man in a row boat must get from point $$A$$ to point $$B$$ on the opposite bank of the river (see figure). The distance $$BC = a.$$ The width of the river $$AC = b.$$ At what minimum speed $$u$$ relative to the still water should the boat travel to reach the point $$B?$$ The velocity of flow of the river is $${v_0}.$$
A.
$$\frac{{\sqrt {{a^2} + {b^2}} }}{{{v_0}}}$$
B.
$$\frac{{{v_0}b}}{{\sqrt {{a^2} + {b^2}} }}$$
C.
$$\frac{{{v_0}a}}{b}$$
D.
$$\frac{{{v_0}a}}{a}$$
Answer :
$$\frac{{{v_0}b}}{{\sqrt {{a^2} + {b^2}} }}$$
Solution :
Suppose $$u$$ is the speed of the boat relative to water, then velocity of the flow (w.r.t bank) $${V_0}$$
$${v_x} = \left( {u\cos \theta + {v_0}} \right)$$ and perpendicular to flow will be $${v_y} = u\sin \theta .$$ Time to cross the river, $$t = \frac{b}{{u\sin \theta }}.$$ In the time the distance travelled by the boat in the direction of flow
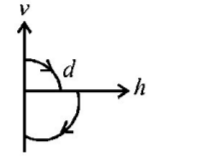
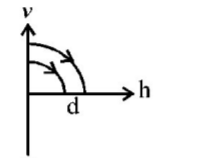
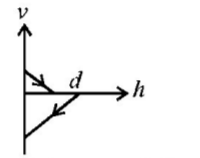
$$\eqalign{ & a = {v_x}t = \left( {u\cos \theta + {v_0}} \right)\frac{b}{{u\sin \theta }} \cr & {\text{or}}\,au\sin \theta = ub\cos \theta + {v_0}b \cr & \therefore u = \frac{{{v_0}b}}{{\left( {a\sin \theta - b\cos \theta } \right)}}.....\left( {\text{i}} \right)\,u\,{\text{to}}\,{\text{be}}\,{\text{minimum}}\,{\text{duld}} \cr & \theta = 0\,{\text{or}}\,\frac{d}{{d\theta }}\left[ {\frac{{{v_0}b}}{{a\sin \theta - b\cos \theta }}} \right] = 0 \cr & {\text{or}}\,\tan \theta = - \frac{a}{b} \cr & \therefore \cos \theta = \frac{b}{{\sqrt {{a^2} + {b^2}} }} \cr} $$
On substituting these values in equation (i), we get
$${u_{\min }} = \frac{{{V_0}b}}{{\sqrt {{a^2} + {b^2}} }}$$
Suppose $$u$$ is the speed of the boat relative to water, then velocity of the flow (w.r.t bank) $${V_0}$$
$${v_x} = \left( {u\cos \theta + {v_0}} \right)$$ and perpendicular to flow will be $${v_y} = u\sin \theta .$$ Time to cross the river, $$t = \frac{b}{{u\sin \theta }}.$$ In the time the distance travelled by the boat in the direction of flow
$$\eqalign{ & a = {v_x}t = \left( {u\cos \theta + {v_0}} \right)\frac{b}{{u\sin \theta }} \cr & {\text{or}}\,au\sin \theta = ub\cos \theta + {v_0}b \cr & \therefore u = \frac{{{v_0}b}}{{\left( {a\sin \theta - b\cos \theta } \right)}}.....\left( {\text{i}} \right)\,u\,{\text{to}}\,{\text{be}}\,{\text{minimum}}\,{\text{duld}} \cr & \theta = 0\,{\text{or}}\,\frac{d}{{d\theta }}\left[ {\frac{{{v_0}b}}{{a\sin \theta - b\cos \theta }}} \right] = 0 \cr & {\text{or}}\,\tan \theta = - \frac{a}{b} \cr & \therefore \cos \theta = \frac{b}{{\sqrt {{a^2} + {b^2}} }} \cr} $$
On substituting these values in equation (i), we get
$${u_{\min }} = \frac{{{V_0}b}}{{\sqrt {{a^2} + {b^2}} }}$$