Question
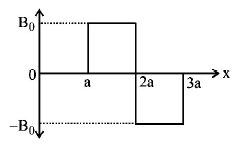
A magnetic field $$\overrightarrow B = {B_0}\hat j,$$ exists in the region $$a < x < 2a,$$ and $$\overrightarrow B = - {B_0}\hat j,$$ in the region $$2a < x < 3a,$$ where $${B_0}$$ is a positive constant. A positive point charge moving with a velocity $$v = {v_0}\hat i,$$ where $${v_0}$$ is a positive constant, enters the magnetic field at $$x = a.$$ The trajectory of the charge in this region can be like
A magnetic field $$\overrightarrow B = {B_0}\hat j,$$ exists in the region $$a < x < 2a,$$ and $$\overrightarrow B = - {B_0}\hat j,$$ in the region $$2a < x < 3a,$$ where $${B_0}$$ is a positive constant. A positive point charge moving with a velocity $$v = {v_0}\hat i,$$ where $${v_0}$$ is a positive constant, enters the magnetic field at $$x = a.$$ The trajectory of the charge in this region can be like
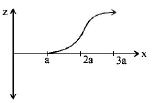
A.

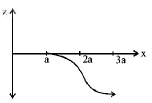
B.

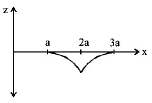
C.


D.

Answer :


Solution :
Use the vector form of $$B$$ and $$v$$ in the formulae $$\overrightarrow F = q\left( {\overrightarrow v \times \overrightarrow B } \right)$$ to get the instantaneous direction of force at $$x = a$$ and $$x = 2a.$$
Use the vector form of $$B$$ and $$v$$ in the formulae $$\overrightarrow F = q\left( {\overrightarrow v \times \overrightarrow B } \right)$$ to get the instantaneous direction of force at $$x = a$$ and $$x = 2a.$$