Question
A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is $${60^ \circ }$$ and one of the fields has a magnitude of $$1.2 \times {10^{ - 2}}T.$$ If the dipole comes to stable equilibrium at an angle of $${15^ \circ }$$ with this field, what is the magnitude of other field ?
A.
$$4.4 \times {10^{ - 3}}\,tesla$$
B.
$$5.2 \times {10^{ - 3}}\,tesla$$
C.
$$3.4 \times {10^{ - 3}}\,tesla$$
D.
$$7.8 \times {10^{ - 3}}\,tesla$$
Answer :
$$4.4 \times {10^{ - 3}}\,tesla$$
Solution :
Given that : $${B_1} = 1.2 \times {10^{ - 2}}T,$$ orientation of dipole with the field $${B_1},{\theta _1} = {15^ \circ }$$
Hence, orientation of dipole with $${B_2},{\theta _2} = {60^ \circ } - {15^ \circ } = {45^ \circ }\left( {{\text{figure}}} \right)$$
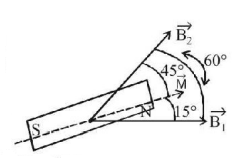
As the dipole is in equilibrium, therefore, the torque on the dipole due to the two fields must be equal and opposite.
If $$M$$ be the magnetic dipole moment of the dipole, then
$$\eqalign{ & {\tau _1} = {\tau _2}\,{\text{or}}\,M{B_1}\sin {\theta _1} = M{B_2}\sin {\theta _2} \cr & {\text{or,}}\,\,{B_2} = \frac{{{B_1}\sin {\theta _1}}}{{\sin {\theta _2}}} = \frac{{1.2 \times {{10}^{ - 2}}\sin {{15}^ \circ }}}{{\sin {{45}^ \circ }}} \cr & = \frac{{1.2 \times {{10}^{ - 2}} \times 0.2588}}{{0.7071}} = 4.4 \times {10^{ - 3}}\,Tesla \cr} $$
Given that : $${B_1} = 1.2 \times {10^{ - 2}}T,$$ orientation of dipole with the field $${B_1},{\theta _1} = {15^ \circ }$$
Hence, orientation of dipole with $${B_2},{\theta _2} = {60^ \circ } - {15^ \circ } = {45^ \circ }\left( {{\text{figure}}} \right)$$

As the dipole is in equilibrium, therefore, the torque on the dipole due to the two fields must be equal and opposite.
If $$M$$ be the magnetic dipole moment of the dipole, then
$$\eqalign{ & {\tau _1} = {\tau _2}\,{\text{or}}\,M{B_1}\sin {\theta _1} = M{B_2}\sin {\theta _2} \cr & {\text{or,}}\,\,{B_2} = \frac{{{B_1}\sin {\theta _1}}}{{\sin {\theta _2}}} = \frac{{1.2 \times {{10}^{ - 2}}\sin {{15}^ \circ }}}{{\sin {{45}^ \circ }}} \cr & = \frac{{1.2 \times {{10}^{ - 2}} \times 0.2588}}{{0.7071}} = 4.4 \times {10^{ - 3}}\,Tesla \cr} $$