Releted MCQ Question on
Optics and Wave >> Ray Optics
Releted Question 1
When a ray of light enters a glass slab from air,
A.
Its wavelength decreases.
B.
Its wavelength increases.
C.
Its frequency decreases.
D.
neither its wavelength nor its frequency changes.
Releted Question 2
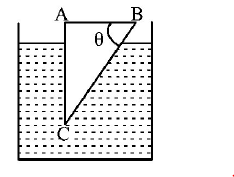
A glass prism of refractive index 1.5 is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if
A glass prism of refractive index 1.5 is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if
A.
$$\sin \theta \geqslant \frac{8}{9}$$
B.
$$\frac{2}{3} < \sin \theta < \frac{8}{9}$$
C.
$$\sin \theta \leqslant \frac{2}{3}$$
D.
None of these
Releted Question 3
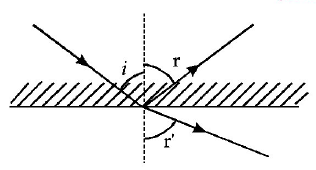
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is
A.
$${\sin ^{ - 1}}\left( {\tan r} \right)$$
B.
$${\sin ^{ - 1}}\left( {\tan i} \right)$$
C.
$${\sin ^{ - 1}}\left( {\tan r'} \right)$$
D.
$${\tan ^{ - 1}}\left( {\sin i} \right)$$
Releted Question 4
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is
A ray of light from a denser medium strike a rarer medium at an angle of incidence $$i$$ (see Fig). The reflected and retracted rays make an angle of $${{{90}^ \circ }}$$ with each other. The angles of reflection and refraction are $$r$$ and $$r’$$ The critical angle is

A.
$${\sin ^{ - 1}}\left( {\tan r} \right)$$
B.
$${\sin ^{ - 1}}\left( {\tan i} \right)$$
C.
$${\sin ^{ - 1}}\left( {\tan r'} \right)$$
D.
$${\tan ^{ - 1}}\left( {\sin i} \right)$$