Question
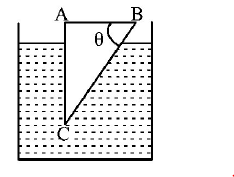
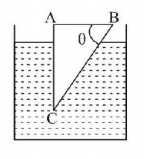
A glass prism of refractive index $$1.5$$ is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if
A glass prism of refractive index $$1.5$$ is immersed in water (refractive index $$\frac{4}{3}$$ ). A light beam incident normally on the face $$AB$$ is totally reflected to reach on the face $$BC$$ if
A.
$$\sin \theta \geqslant \frac{8}{9}$$
B.
$$\frac{2}{3} < \sin \theta < \frac{8}{9}$$
C.
$$\sin \theta \leqslant \frac{2}{3}$$
D.
$$\frac{1}{2} < \sin \theta < 1$$
Answer :
$$\sin \theta \geqslant \frac{8}{9}$$
Solution :
The phenomenon of total internal reflection takes place during reflection at $$P.$$
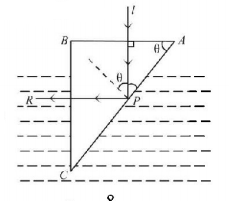
$$\sin \theta = \frac{1}{{_g^w\mu }}\,......\left( {\text{i}} \right)$$
Now,
$$\eqalign{ & _g^w\mu = \frac{{_g^a\mu }}{{_w^a\mu }} = \frac{{1.5}}{{\frac{4}{3}}} = 1.125 \cr & \therefore \sin \theta = \frac{1}{{1.125}} = \frac{8}{9} \cr & \therefore \sin \theta \,{\text{should}}\,{\text{be}}\,{\text{greater}}\,{\text{than}}\,\frac{8}{9}. \cr} $$
The phenomenon of total internal reflection takes place during reflection at $$P.$$

$$\sin \theta = \frac{1}{{_g^w\mu }}\,......\left( {\text{i}} \right)$$
Now,
$$\eqalign{ & _g^w\mu = \frac{{_g^a\mu }}{{_w^a\mu }} = \frac{{1.5}}{{\frac{4}{3}}} = 1.125 \cr & \therefore \sin \theta = \frac{1}{{1.125}} = \frac{8}{9} \cr & \therefore \sin \theta \,{\text{should}}\,{\text{be}}\,{\text{greater}}\,{\text{than}}\,\frac{8}{9}. \cr} $$