Question
A disc of mass $$M$$ and radius $$R$$ is rolling with angular speed $$\omega $$ on a horizontal plane as shown in Figure. The magnitude of angular momentum of the disc about the origin $$O$$ is
A disc of mass $$M$$ and radius $$R$$ is rolling with angular speed $$\omega $$ on a horizontal plane as shown in Figure. The magnitude of angular momentum of the disc about the origin $$O$$ is
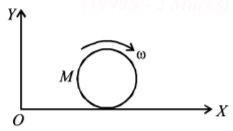
A.
$$\left( {\frac{1}{2}} \right)M{R^2}\omega $$
B.
$$M{R^2}\omega $$
C.
$$\left( {\frac{3}{2}} \right)M{R^2}\omega $$
D.
$$2M{R^2}\omega $$
Answer :
$$\left( {\frac{3}{2}} \right)M{R^2}\omega $$
Solution :
KEY CONCEPT
The disc has two types of motion namely translational and rotational. Therefore there are two types of angular momentum and the total angular momentum is the vector sum of these two.
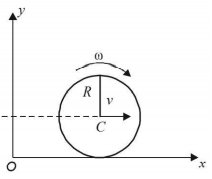
In this case both the angular momentum have the same direction (perpendicular to the plane of paper and away from the reader).
$$\vec L = {{\vec L}_T} + {{\vec L}_R}$$
$${L_T} = $$ angular momentum due to translational motion.
$${L_R} = $$ angular momentum due to rotational motion about $$C.M.$$
$$L = MV \times R + {I_{cm}}\omega $$
$${I_{cm}} = M.I.$$ about centre of mass C.
$$ = M\left( {R\,\omega } \right) + \frac{1}{2}M{R^2}\,\omega $$
($$v = R\omega $$ in case of rolling motion and surface at rest)
$$ = \frac{3}{2}M{R^2}\,\omega $$
KEY CONCEPT
The disc has two types of motion namely translational and rotational. Therefore there are two types of angular momentum and the total angular momentum is the vector sum of these two.

In this case both the angular momentum have the same direction (perpendicular to the plane of paper and away from the reader).
$$\vec L = {{\vec L}_T} + {{\vec L}_R}$$
$${L_T} = $$ angular momentum due to translational motion.
$${L_R} = $$ angular momentum due to rotational motion about $$C.M.$$
$$L = MV \times R + {I_{cm}}\omega $$
$${I_{cm}} = M.I.$$ about centre of mass C.
$$ = M\left( {R\,\omega } \right) + \frac{1}{2}M{R^2}\,\omega $$
($$v = R\omega $$ in case of rolling motion and surface at rest)
$$ = \frac{3}{2}M{R^2}\,\omega $$