Releted MCQ Question on
Heat and Thermodynamics >> Conduction
Releted Question 1
A wall has two layers $$A$$ and $$B,$$ each made of different material. Both the layers have the same thickness. The thermal conductivity of the meterial of $$A$$ is twice that of $$B.$$ Under thermal equilibrium, the temperature difference across the wall is $${36^ \circ }C.$$ The temperature difference across the layer $$A$$ is
A.
$${6^ \circ }C$$
B.
$${12^ \circ }C$$
C.
$${18^ \circ }C$$
D.
$${24^ \circ }C$$
Releted Question 2
Three rods of identical cross - sectional area and made from the same metal from the sides of an isosceles triangle $$ABC,$$ right - angled at $$B.$$ The points $$A$$ and $$B$$ are maintained at temperatures $$T$$ and $$\left( {\sqrt 2 } \right)$$ $$T$$ respectively. In the steady state, the temperature of the point $$C$$ is $${T_c}.$$ Assuming that only heat conduction takes place, $$\frac{{{T_c}}}{T}$$ is
A.
$$\frac{1}{{2\left( {\sqrt 2 - 1} \right)}}$$
B.
$$\frac{3}{{\sqrt 2 + 1}}$$
C.
$$\frac{1}{{\sqrt 3 \left( {\sqrt 2 - 1} \right)}}$$
D.
$$\frac{1}{{\sqrt 2 + 1}}$$
Releted Question 3
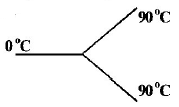
Three rods made of same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at $${0^ \circ }C$$ and $${90^ \circ }C$$ respectively. The temperature of the junction of the three rods will be
Three rods made of same material and having the same cross-section have been joined as shown in the figure. Each rod is of the same length. The left and right ends are kept at $${0^ \circ }C$$ and $${90^ \circ }C$$ respectively. The temperature of the junction of the three rods will be
A.
$${45^ \circ }C$$
B.
$${60^ \circ }C$$
C.
$${30^ \circ }C$$
D.
$${20^ \circ }C$$
Releted Question 4
Two identical rods are connected between two containers one of them is at $${100^ \circ }C$$ and another is at $${0^ \circ }C.$$ If rods are connected in parallel then the rate of melting of ice is $${q_1}\,gm/sec.$$ If they are connected in series then the rate is $${{q_2}}.$$ The ratio $$\frac{{{q_2}}}{{{q_1}}}$$ is
A.
2
B.
4
C.
$$\frac{1}{2}$$
D.
$$\frac{1}{4}$$