Question
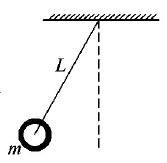
A conical pendulum of length $$1\,m$$ makes an angle $$\theta = {45^ \circ }$$ w.r.t. $$Z$$-axis and moves in a circle in the $$XY$$ plane. The radius of the circle is $$0.4\,m$$ and its centre is vertically below $$O.$$ The speed of the pendulum, in its circular path, will be:
A conical pendulum of length $$1\,m$$ makes an angle $$\theta = {45^ \circ }$$ w.r.t. $$Z$$-axis and moves in a circle in the $$XY$$ plane. The radius of the circle is $$0.4\,m$$ and its centre is vertically below $$O.$$ The speed of the pendulum, in its circular path, will be:
(Take $$g = 10\,m{s^{ - 2}}$$ )

A.
$$0.4\,m/s$$
B.
$$4\,m/s$$
C.
$$0.2\,m/s$$
D.
$$2\,m/s$$
Answer :
$$2\,m/s$$
Solution :

$$\eqalign{ & {\text{Given,}}\,\,\theta = {45^ \circ },\,r = 0.4\,m,\,g = 10\,m/{s^2} \cr & T\sin \theta = \frac{{m{v^2}}}{r}\,......\left( {\text{i}} \right) \cr & T\cos \theta = mg\,......\left( {{\text{ii}}} \right) \cr} $$
From equation (i) & (ii) we have,
$$\eqalign{ & \tan \theta = \frac{{{v^2}}}{{rg}} \cr & {v^2} = rg\quad \cr & \because \theta = {45^ \circ } \cr} $$
Hence, speed of the pendulum in its circular path,
$$v = \sqrt {rg} = \sqrt {0.4 \times 10} = 2\,m/s$$

$$\eqalign{ & {\text{Given,}}\,\,\theta = {45^ \circ },\,r = 0.4\,m,\,g = 10\,m/{s^2} \cr & T\sin \theta = \frac{{m{v^2}}}{r}\,......\left( {\text{i}} \right) \cr & T\cos \theta = mg\,......\left( {{\text{ii}}} \right) \cr} $$
From equation (i) & (ii) we have,
$$\eqalign{ & \tan \theta = \frac{{{v^2}}}{{rg}} \cr & {v^2} = rg\quad \cr & \because \theta = {45^ \circ } \cr} $$
Hence, speed of the pendulum in its circular path,
$$v = \sqrt {rg} = \sqrt {0.4 \times 10} = 2\,m/s$$