Question
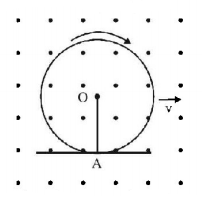
A conducting ring of radius $$r$$ with a conducting spoke $$OA$$ is in pure rolling on a horizontal horizontal surface in a region having a uniform magnetic field $$B$$ as shown, $$v$$ being the velocity of the centre of the ring. Then the potential difference $${V_0} - {V_A}$$ is :
A conducting ring of radius $$r$$ with a conducting spoke $$OA$$ is in pure rolling on a horizontal horizontal surface in a region having a uniform magnetic field $$B$$ as shown, $$v$$ being the velocity of the centre of the ring. Then the potential difference $${V_0} - {V_A}$$ is :
A.
$$\frac{{Bvr}}{2}$$
B.
$$\frac{{3Bvr}}{2}$$
C.
$$ - \frac{{Bvr}}{2}$$
D.
$$\frac{{ - 3Bvr}}{2}$$
Answer :
$$ - \frac{{Bvr}}{2}$$
Solution :
Considering pure rolling of $$OA$$ about $$A$$ : the induced emf across $$OA$$ will be:
$$\left| {\overrightarrow e } \right| = \frac{{B\omega {{\left( r \right)}^2}}}{2}.$$
From lenz law, $$O$$ will be the negative end, while $$A$$ will be the positive end.
Hence $${V_0} - {V_A} = - \frac{{B\omega {r^2}}}{2}$$
$$\eqalign{ & {\text{And}}\,\,v = \omega r \cr & \Rightarrow {V_0} - {V_A} = - \frac{{Bvr}}{2} \cr} $$
Considering pure rolling of $$OA$$ about $$A$$ : the induced emf across $$OA$$ will be:
$$\left| {\overrightarrow e } \right| = \frac{{B\omega {{\left( r \right)}^2}}}{2}.$$
From lenz law, $$O$$ will be the negative end, while $$A$$ will be the positive end.
Hence $${V_0} - {V_A} = - \frac{{B\omega {r^2}}}{2}$$
$$\eqalign{ & {\text{And}}\,\,v = \omega r \cr & \Rightarrow {V_0} - {V_A} = - \frac{{Bvr}}{2} \cr} $$
