Question
A conducting disc of conductivity $$\sigma $$ has a radius $$'a'$$ and thickness $$'t'.$$ If the magnetic field $$B$$ is applied in a direction perpendicular to the plane of the disc changes with time at the rate of $$\frac{{dB}}{{dt}} = \alpha .$$ Calculate the power dissipated in the disc due to the induced current.
A.
$$\frac{{\pi t\sigma {a^4}}}{8}{\alpha ^2}$$
B.
$$\frac{{\pi t\sigma {a^4}}}{4}{\alpha ^2}$$
C.
$$\frac{{\pi t\sigma {a^4}}}{2}{\alpha ^2}$$
D.
$$\frac{{2\pi t\sigma {a^4}}}{3}{\alpha ^2}$$
Answer :
$$\frac{{\pi t\sigma {a^4}}}{8}{\alpha ^2}$$
Solution :
Consider an elemental circle of thickness $$dr.$$
The induced emf in the circular path of radius $$r$$ is
$$\varepsilon = \frac{d}{{dt}}\left( {\pi {r^2}B} \right) = \pi {r^2}\alpha $$
The resistance of circular path is
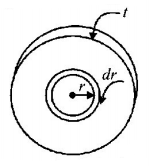
The length of the path being $$2\pi r$$ and $$tdr$$ is the cross sectional area of current flow. For the element the power dissipated inside the path is
$$dP = \frac{{{\varepsilon ^2}}}{R} = \frac{{\pi t\sigma }}{2}{\alpha ^2}{r^3}dr$$
The total dissipated power $$P$$ is
$$P = \frac{{\pi t\sigma }}{2}{\alpha ^2}\int\limits_0^a {{r^3}dr} = \frac{{\pi t\sigma {a^4}}}{8}{\alpha ^2}$$
Consider an elemental circle of thickness $$dr.$$
The induced emf in the circular path of radius $$r$$ is
$$\varepsilon = \frac{d}{{dt}}\left( {\pi {r^2}B} \right) = \pi {r^2}\alpha $$
The resistance of circular path is

The length of the path being $$2\pi r$$ and $$tdr$$ is the cross sectional area of current flow. For the element the power dissipated inside the path is
$$dP = \frac{{{\varepsilon ^2}}}{R} = \frac{{\pi t\sigma }}{2}{\alpha ^2}{r^3}dr$$
The total dissipated power $$P$$ is
$$P = \frac{{\pi t\sigma }}{2}{\alpha ^2}\int\limits_0^a {{r^3}dr} = \frac{{\pi t\sigma {a^4}}}{8}{\alpha ^2}$$
