Question
A coaxial cable consists of a thin inner conductor fixed along the axis of a hollow outer conductor. The two conductors carry equal currents in opposites directions. Let $${B_1}$$ and $${B_2}$$ be the magnetic fields in the region between the conductors and outside the conductor, respectively Then,
A.
$${B_1} \ne 0,{B_2} \ne 0$$
B.
$${B_1} = {B_2} = 0$$
C.
$${B_1} \ne 0,{B_2} = 0$$
D.
$${B_1} = 0,{B_2} \ne 0$$
Answer :
$${B_1} \ne 0,{B_2} = 0$$
Solution :
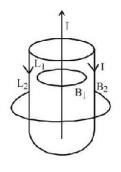
Apply Ampere's circular law to the coaxial circular loops $${L_1}$$ and $${L_2}.$$ The magnetic field is $${B_1}$$ at all points on $${L_1}$$ and $${B_2}$$ at all points on $${L_2}.$$ $$\sum I \ne 0$$ for $${L_1}$$ and 0 for $${L_2}.$$
Hence, $${B_1} \ne 0$$ but $${B_2} = 0$$
$$\left[ {{\text{As}}\,\oint {\vec B.d\vec i = {\mu _0}\sum I} } \right]$$

Apply Ampere's circular law to the coaxial circular loops $${L_1}$$ and $${L_2}.$$ The magnetic field is $${B_1}$$ at all points on $${L_1}$$ and $${B_2}$$ at all points on $${L_2}.$$ $$\sum I \ne 0$$ for $${L_1}$$ and 0 for $${L_2}.$$
Hence, $${B_1} \ne 0$$ but $${B_2} = 0$$
$$\left[ {{\text{As}}\,\oint {\vec B.d\vec i = {\mu _0}\sum I} } \right]$$