Question
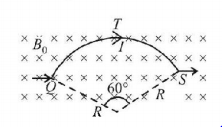
A circular arc $$QTS$$ is kept in an external magnetic field $${{\vec B}_0}$$ as shown in figure. The arc carries a current $$I.$$ The magnetic field is directed normal and into the page. The force acting on the arc is
A circular arc $$QTS$$ is kept in an external magnetic field $${{\vec B}_0}$$ as shown in figure. The arc carries a current $$I.$$ The magnetic field is directed normal and into the page. The force acting on the arc is
A.
$$2I{B_0}R\hat k$$
B.
$$I{B_0}R\hat k$$
C.
$$ - 2I{B_0}R\hat k$$
D.
$$ - I{B_0}R\hat k$$
Answer :
$$I{B_0}R\hat k$$
Solution :
We know, $$\vec F = I\left( {\vec \ell \times \vec B} \right)\,\,{\text{or}}\,\,d\vec F = IBd\ell \sin \theta $$
$$\eqalign{ & \therefore F = \int_{{{60}^ \circ }}^{{{120}^ \circ }} {I{B_0}d\ell \,\sin \theta d\ell } \,\,{\text{where,}}\,d\ell = rd\theta \cr & F = \int_{{{60}^ \circ }}^{{{120}^ \circ }} {I{B_0}} R\sin \theta d\theta = IBR\left[ { - \cos \theta } \right]_{{{60}^ \circ }}^{{{120}^ \circ }} \cr & = I{B_0}R\left[ { - \left( { - \frac{1}{2}} \right) + \left( {\frac{1}{2}} \right)} \right] = I{B_0}R \cr} $$
Hence, force acting on the arc is $$I{B_0}R\,\hat k.$$
We know, $$\vec F = I\left( {\vec \ell \times \vec B} \right)\,\,{\text{or}}\,\,d\vec F = IBd\ell \sin \theta $$
$$\eqalign{ & \therefore F = \int_{{{60}^ \circ }}^{{{120}^ \circ }} {I{B_0}d\ell \,\sin \theta d\ell } \,\,{\text{where,}}\,d\ell = rd\theta \cr & F = \int_{{{60}^ \circ }}^{{{120}^ \circ }} {I{B_0}} R\sin \theta d\theta = IBR\left[ { - \cos \theta } \right]_{{{60}^ \circ }}^{{{120}^ \circ }} \cr & = I{B_0}R\left[ { - \left( { - \frac{1}{2}} \right) + \left( {\frac{1}{2}} \right)} \right] = I{B_0}R \cr} $$
Hence, force acting on the arc is $$I{B_0}R\,\hat k.$$