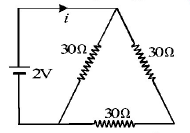
Question
A cell having an emf $$\varepsilon $$ and internal resistance $$r$$ is connected across a variable external resistance $$R.$$ As the resistance $$R$$ is increased, the plot of potential difference $$V$$ across $$R$$ is given by
A.
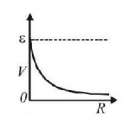

B.


C.
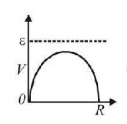

D.
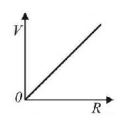

Answer :


Solution :
Current in the circuit,
$$I = \frac{\varepsilon }{{R + r}}$$
Potential difference across $$R,$$
$$\eqalign{ & V = IR = \left( {\frac{\varepsilon }{{R + r}}} \right)R = \frac{\varepsilon }{{1 + \frac{r}{R}}} \cr & {\text{When}}\,R = 0,V = 0 \cr & R = \infty ,V = \varepsilon \cr} $$
Current in the circuit,
$$I = \frac{\varepsilon }{{R + r}}$$
Potential difference across $$R,$$
$$\eqalign{ & V = IR = \left( {\frac{\varepsilon }{{R + r}}} \right)R = \frac{\varepsilon }{{1 + \frac{r}{R}}} \cr & {\text{When}}\,R = 0,V = 0 \cr & R = \infty ,V = \varepsilon \cr} $$