Question
A car accelerates from rest with a constant acceleration $$\alpha $$ on a straight road. After gaining a velocity $${v_1}$$ the car moves with the same velocity for some-time. Then the car decelerated to rest with a retardation $$\beta .$$ If the total distance covered by the car is equal to $$S,$$ the total time taken for its motion is
A.
$$\frac{S}{v} + \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right)$$
B.
$$\frac{S}{v} + \frac{v}{\alpha } + \frac{v}{\beta }$$
C.
$$\left( {\frac{v}{\alpha } + \frac{v}{\beta }} \right)$$
D.
$$\frac{S}{v} - \frac{v}{2}\left( {\frac{v}{\alpha } + \frac{v}{\beta }} \right)$$
Answer :
$$\frac{S}{v} + \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right)$$
Solution :
From $$v = u + at,$$ we have
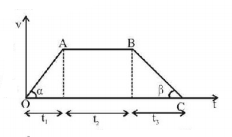
$$\eqalign{ & v = 0 + \alpha {t_1} \Rightarrow {t_1} = \frac{v}{\alpha } \cr & 0 = v - \beta {t_3} \Rightarrow {t_3} = \frac{v}{\beta }. \cr} $$
$$\eqalign{ & {\text{Now,}}\,\,S = \frac{1}{2}v{t_1} + v{t_2} + \frac{1}{2}v{t_3} = \frac{{{v^2}}}{{2\alpha }} + v{t_2} + \frac{{{v^2}}}{{2\beta }} \cr & \Rightarrow {t_2} = \frac{S}{v} - \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right). \cr & {\text{Hence,}}\,\,{t_1} + {t_2} + {t_3} = \frac{S}{v} + \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right) \cr} $$
From $$v = u + at,$$ we have

$$\eqalign{ & v = 0 + \alpha {t_1} \Rightarrow {t_1} = \frac{v}{\alpha } \cr & 0 = v - \beta {t_3} \Rightarrow {t_3} = \frac{v}{\beta }. \cr} $$
$$\eqalign{ & {\text{Now,}}\,\,S = \frac{1}{2}v{t_1} + v{t_2} + \frac{1}{2}v{t_3} = \frac{{{v^2}}}{{2\alpha }} + v{t_2} + \frac{{{v^2}}}{{2\beta }} \cr & \Rightarrow {t_2} = \frac{S}{v} - \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right). \cr & {\text{Hence,}}\,\,{t_1} + {t_2} + {t_3} = \frac{S}{v} + \frac{v}{2}\left( {\frac{1}{\alpha } + \frac{1}{\beta }} \right) \cr} $$