Question
A bus travelling the first one-third distance at a speed of $$10\,km/h,$$ the next one-third at $$20\,km/h$$ and the last one-third at $$60\,km/h.$$ The average speed of the bus is
A.
$$9\,km/h$$
B.
$$16\,km/h$$
C.
$$18\,km/h$$
D.
$$48\,km/h$$
Answer :
$$18\,km/h$$
Solution :
Average speed can be calculated as the total distance travelled divided by the total time taken.
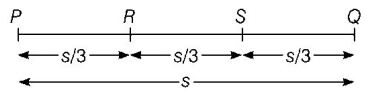
Let $${t_1},{t_2},{t_3}$$ be times taken in covering distances $$PR, RS$$ and $$SQ$$ respectively.
$$\eqalign{ & \therefore {t_1} = \frac{{\left( {\frac{s}{3}} \right)}}{{10}}, \cr & {t_2} = \frac{{\left( {\frac{s}{3}} \right)}}{{20}} \cr & {\text{and}}\,\,{t_3} = \frac{{\left( {\frac{s}{3}} \right)}}{{60}} \cr & \therefore {\text{Average speed}} = \frac{{{\text{Total distance}}}}{{{\text{Total time}}}} \cr & = \frac{s}{{{t_1} + {t_2} + {t_3}}} \cr & = \frac{s}{{\frac{{\left( {\frac{s}{3}} \right)}}{{10}} + \frac{{\left( {\frac{s}{3}} \right)}}{{20}} + \frac{{\left( {\frac{s}{3}} \right)}}{{60}}}} \cr & = \frac{s}{{\left( {\frac{s}{{18}}} \right)}} \cr & = 18\,km/h \cr} $$
Average speed can be calculated as the total distance travelled divided by the total time taken.

Let $${t_1},{t_2},{t_3}$$ be times taken in covering distances $$PR, RS$$ and $$SQ$$ respectively.
$$\eqalign{ & \therefore {t_1} = \frac{{\left( {\frac{s}{3}} \right)}}{{10}}, \cr & {t_2} = \frac{{\left( {\frac{s}{3}} \right)}}{{20}} \cr & {\text{and}}\,\,{t_3} = \frac{{\left( {\frac{s}{3}} \right)}}{{60}} \cr & \therefore {\text{Average speed}} = \frac{{{\text{Total distance}}}}{{{\text{Total time}}}} \cr & = \frac{s}{{{t_1} + {t_2} + {t_3}}} \cr & = \frac{s}{{\frac{{\left( {\frac{s}{3}} \right)}}{{10}} + \frac{{\left( {\frac{s}{3}} \right)}}{{20}} + \frac{{\left( {\frac{s}{3}} \right)}}{{60}}}} \cr & = \frac{s}{{\left( {\frac{s}{{18}}} \right)}} \cr & = 18\,km/h \cr} $$