Releted MCQ Question on
Basic Physics >> Impulse
Releted Question 1
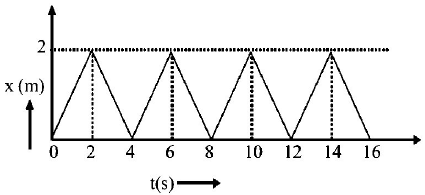
The figure shows the position-time $$\left( {x - t} \right)$$ graph of one dimensional motion of a body of mass $$0.4kg.$$ The magnitude of each impulse is
The figure shows the position-time $$\left( {x - t} \right)$$ graph of one dimensional motion of a body of mass $$0.4kg.$$ The magnitude of each impulse is
A.
$$0.4Ns$$
B.
$$0.8Ns$$
C.
$$1.6Ns$$
D.
$$0.2Ns$$
Releted Question 2
A rigid ball of mass $$m$$ strikes a rigid wall at $${60^ \circ }$$ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wall on the ball will be
A rigid ball of mass $$m$$ strikes a rigid wall at $${60^ \circ }$$ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wall on the ball will be

A.
$$mv$$
B.
$$2mv$$
C.
$$\frac{{mv}}{2}$$
D.
$$\frac{{mv}}{3}$$
Releted Question 3
The force $$F$$ acting on a particle of mass $$m$$ is indicated by the force-time graph shown below. The change in momentum of the particle over the time interval from $$0$$ to $$8 s$$ is
The force $$F$$ acting on a particle of mass $$m$$ is indicated by the force-time graph shown below. The change in momentum of the particle over the time interval from $$0$$ to $$8 s$$ is

A.
$$24\,N{\text{-}}s$$
B.
$$20\,N{\text{-}}s$$
C.
$$12\,N{\text{-}}s$$
D.
$$6\,N{\text{-}}s$$
Releted Question 4
A man of $$50\,kg$$ mass is standing in a gravity free space at a height of $$10\,m$$ above the floor. He throws a stone of $$0.5\,kg$$ mass downwards with a speed $$2\,m{s^{ - 1}}.$$ When the stone reaches the floor, the distance of the man above the floor will be
A.
$$9.9\,m$$
B.
$$10.1\,m$$
C.
$$10\,m$$
D.
$$20\,m$$