Releted MCQ Question on
Basic Physics >> Momentum
Releted Question 1
Two particles of masses $${m_1}$$ and $${m_2}$$ in projectile motion have velocities $${{\vec v}_1}$$ and $${{\vec v}_2}$$ respectively at time $$t = 0.$$ They collide at time $${t_0.}$$ Their velocities become $${{\vec v}_1}'$$ and $${{\vec v}_2}'$$ at time $$2{t_0}$$ while still moving in the air. The value of $$\left| {\left( {{m_1}{{\vec v}_1}' + {m_2}{{\vec v}_2}'} \right) - \left( {{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2}} \right)} \right|$$ is
A.
zero
B.
$$\left( {{m_1} + {m_2}} \right)g{t_0}$$
C.
$$\frac{1}{2}\left( {{m_1} + {m_2}} \right)g{t_0}$$
D.
$$2\left( {{m_1} + {m_2}} \right)g{t_0}$$
Releted Question 2
Two blocks of masses $$10kg$$ and $$4kg$$ are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of $$14 m/s$$ to the heavier block in the direction of the lighter block. The velocity of the centre of mass is
A.
$$30 m/s$$
B.
$$20 m/s$$
C.
$$10 m/s$$
D.
$$5 m/s$$
Releted Question 3
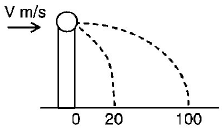
A ball of mass $$0.2kg$$ rests on a vertical post of height $$5m.$$ A bullet of mass $$0.01kg,$$ traveling with a velocity $$V m/s$$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $$20m$$ and the bullet at a distance of $$100m$$ from the foot of the post. The velocity $$V$$ of the bullet is
A ball of mass $$0.2kg$$ rests on a vertical post of height $$5m.$$ A bullet of mass $$0.01kg,$$ traveling with a velocity $$V m/s$$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $$20m$$ and the bullet at a distance of $$100m$$ from the foot of the post. The velocity $$V$$ of the bullet is
A.
$$250 m/s$$
B.
$$250\sqrt 2 \,m/s$$
C.
$$400 m/s$$
D.
$$500 m/s$$
Releted Question 4
A particle of mass $$m$$ is projected from the ground with an initial speed $${u_0}$$ at an angle $$\alpha $$ with the horizontal. At the highest point of its trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed $${u_0}.$$ The angle that the composite system makes with the horizontal immediately after the collision is
A.
$$\frac{\pi }{4}$$
B.
$$\frac{\pi }{4} + \alpha $$
C.
$$\frac{\pi }{2} - \alpha $$
D.
$$\frac{\pi }{2}$$