Question
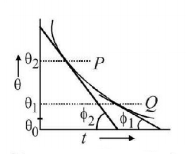
A body cools in a surrounding which is at a constant temperature of $${\theta _0}.$$ Assume that it obeys Newton’s law of cooling. Its temperature $$\theta $$ is plotted against time $$t.$$ Tangents are drawn to the curve at the points $$P\left( {\theta = {\theta _2}} \right)$$ and $$Q\left( {\theta = {\theta _1}} \right).$$ These tangents meet the time axis at angle of $${\phi _2}$$ and $${\phi _1},$$ as shown, then
A body cools in a surrounding which is at a constant temperature of $${\theta _0}.$$ Assume that it obeys Newton’s law of cooling. Its temperature $$\theta $$ is plotted against time $$t.$$ Tangents are drawn to the curve at the points $$P\left( {\theta = {\theta _2}} \right)$$ and $$Q\left( {\theta = {\theta _1}} \right).$$ These tangents meet the time axis at angle of $${\phi _2}$$ and $${\phi _1},$$ as shown, then
A.
$$\frac{{\tan {\phi _2}}}{{\tan {\phi _1}}} = \frac{{{\theta _1} - {\theta _0}}}{{{\theta _2} - {\theta _0}}}$$
B.
$$\frac{{\tan {\phi _2}}}{{\tan {\phi _1}}} = \frac{{{\theta _2} - {\theta _0}}}{{{\theta _1} - {\theta _0}}}$$
C.
$$\frac{{\tan {\phi _1}}}{{\tan {\phi _2}}} = \frac{{{\theta _1}}}{{{\theta _2}}}$$
D.
$$\frac{{\tan {\phi _1}}}{{\tan {\phi _2}}} = \frac{{{\theta _2}}}{{{\theta _1}}}$$
Answer :
$$\frac{{\tan {\phi _2}}}{{\tan {\phi _1}}} = \frac{{{\theta _2} - {\theta _0}}}{{{\theta _1} - {\theta _0}}}$$
Solution :
For $$\theta - t$$ plot, rate of cooling $$ = \frac{{dQ}}{{dt}} = $$ slope of the curve.
$$\eqalign{ & AT\,P,\frac{{dQ}}{{dt}} = \left| {\tan \left( {{{180}^ \circ } - {\phi _2}} \right)} \right| \cr & = \tan {\phi _2} = k\left( {{\theta _2} - {\theta _1}} \right) \cr} $$
where $$k$$ = constant.
At $$Q,$$
$$\eqalign{ & \frac{{dQ}}{{dt}} = \left| {\tan \left( {{{180}^ \circ } - {\varphi _1}} \right)} \right| = \tan {\varphi _1} = k\left( {{\theta _1} - {\theta _0}} \right) \cr & \therefore \frac{{\tan {\phi _2}}}{{\tan {\phi _1}}} = \frac{{{\theta _2} - {\theta _0}}}{{{\theta _1} - {\theta _0}}} \cr} $$
For $$\theta - t$$ plot, rate of cooling $$ = \frac{{dQ}}{{dt}} = $$ slope of the curve.
$$\eqalign{ & AT\,P,\frac{{dQ}}{{dt}} = \left| {\tan \left( {{{180}^ \circ } - {\phi _2}} \right)} \right| \cr & = \tan {\phi _2} = k\left( {{\theta _2} - {\theta _1}} \right) \cr} $$
where $$k$$ = constant.
At $$Q,$$
$$\eqalign{ & \frac{{dQ}}{{dt}} = \left| {\tan \left( {{{180}^ \circ } - {\varphi _1}} \right)} \right| = \tan {\varphi _1} = k\left( {{\theta _1} - {\theta _0}} \right) \cr & \therefore \frac{{\tan {\phi _2}}}{{\tan {\phi _1}}} = \frac{{{\theta _2} - {\theta _0}}}{{{\theta _1} - {\theta _0}}} \cr} $$