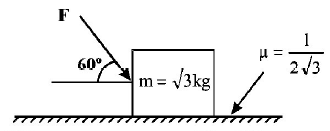
Question
A block of mass $$2kg$$ rests on a rough inclined plane making an angle of $${30^ \circ }$$ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A.
$$9.8N$$
B.
$$0.7 \times 9.8 \times \sqrt 3 N$$
C.
$$9.8 \times \sqrt 3 N$$
D.
$$0.7 \times 9.8N$$
Answer :
$$9.8N$$
Solution :
The force acting on the block along the incline to shift the block downwards

$$ = mg\sin \theta = 2 \times 9.8\sin {30^ \circ } = 9.8N$$
The limiting frictional force
$${f_l} = {\mu _s}mg\cos \theta = 0.7 \times 2 \times 9.8 \times \frac{{\sqrt 3 }}{2} = 11.8N$$
Note : The frictional force is never greater than the force tending to produce relative motion. Therefore the frictional force is $$9 8N.$$
The force acting on the block along the incline to shift the block downwards

$$ = mg\sin \theta = 2 \times 9.8\sin {30^ \circ } = 9.8N$$
The limiting frictional force
$${f_l} = {\mu _s}mg\cos \theta = 0.7 \times 2 \times 9.8 \times \frac{{\sqrt 3 }}{2} = 11.8N$$
Note : The frictional force is never greater than the force tending to produce relative motion. Therefore the frictional force is $$9 8N.$$