Question
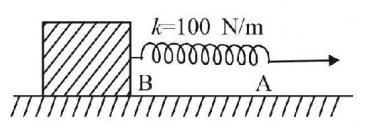
A block lying on a smooth surface with spring connected to it is pulled by an external force as shown. Initially the velocity of ends $$A$$ and $$B$$ of the spring are $$4\,m/s$$ and $$2\,m/s$$ respectively. If the energy of the spring is increasing at the rate of $$20\,J/sec,$$ then the stretch in the spring is
A block lying on a smooth surface with spring connected to it is pulled by an external force as shown. Initially the velocity of ends $$A$$ and $$B$$ of the spring are $$4\,m/s$$ and $$2\,m/s$$ respectively. If the energy of the spring is increasing at the rate of $$20\,J/sec,$$ then the stretch in the spring is
A.
$$1.0\,cm$$
B.
$$2.0\,cm$$
C.
$$10\,cm$$
D.
$$2.0\,cm$$
Answer :
$$10\,cm$$
Solution :
Let $${x_A}$$ and $${x_B}$$ be the position of ends $$A$$ and $$B$$ at time $$t$$ from the block, then stretched length of the spring will be
$${\ell _2} = {x_A} - {x_B}$$
and so the stretch
$$\eqalign{ & \Delta \ell = {\ell _2} - {\ell _1} = \left( {{x_A} - {x_B}} \right) - {\ell _1}\left( {{\ell _1}\,{\text{natural}}\,{\text{length}}\,{\text{of}}\,{\text{the}}\,{\text{spring}}} \right) \cr & {\text{So,}}\,\,U = \frac{1}{2}k\Delta {\ell ^2} = \frac{1}{2}k{\left[ {\left( {{x_A} - {x_B}} \right) - {\ell _1}} \right]^2} \cr & P = \frac{{dU}}{{dt}} = \frac{1}{2}k \cdot 2\left( {{x_A} - {x_B} - {\ell _1}} \right)\left( {\frac{{d{x_A}}}{{dt}} - \frac{{d{x_B}}}{{dt}}} \right) \cr & P = F\left( {{v_A} - {v_B}} \right)\,\,F = \frac{P}{{{v_A} - {v_B}}} \cr & \Delta \ell = \frac{F}{k} = \frac{P}{{\left( {{v_A} - {v_B}} \right)k}} = \frac{{20}}{{\left( {4 - 2} \right) \times 100}} \cr & \Delta \ell = 0.1\,m = 10\,cm \cr} $$
Let $${x_A}$$ and $${x_B}$$ be the position of ends $$A$$ and $$B$$ at time $$t$$ from the block, then stretched length of the spring will be
$${\ell _2} = {x_A} - {x_B}$$
and so the stretch
$$\eqalign{ & \Delta \ell = {\ell _2} - {\ell _1} = \left( {{x_A} - {x_B}} \right) - {\ell _1}\left( {{\ell _1}\,{\text{natural}}\,{\text{length}}\,{\text{of}}\,{\text{the}}\,{\text{spring}}} \right) \cr & {\text{So,}}\,\,U = \frac{1}{2}k\Delta {\ell ^2} = \frac{1}{2}k{\left[ {\left( {{x_A} - {x_B}} \right) - {\ell _1}} \right]^2} \cr & P = \frac{{dU}}{{dt}} = \frac{1}{2}k \cdot 2\left( {{x_A} - {x_B} - {\ell _1}} \right)\left( {\frac{{d{x_A}}}{{dt}} - \frac{{d{x_B}}}{{dt}}} \right) \cr & P = F\left( {{v_A} - {v_B}} \right)\,\,F = \frac{P}{{{v_A} - {v_B}}} \cr & \Delta \ell = \frac{F}{k} = \frac{P}{{\left( {{v_A} - {v_B}} \right)k}} = \frac{{20}}{{\left( {4 - 2} \right) \times 100}} \cr & \Delta \ell = 0.1\,m = 10\,cm \cr} $$