Question
A ball rolls off to the top of a staircase with a horizontal velocity $$u\,m/s.$$ If the steps are $$h$$ metre high and $$b$$ metre wide, the ball will hit the edge of the $${n^{th}}$$ step, if
A.
$$n = \frac{{2hu}}{{g{b^2}}}$$
B.
$$n = \frac{{2h{u^2}}}{{gb}}$$
C.
$$n = \frac{{2h{u^2}}}{{g{b^2}}}$$
D.
$$n = \frac{{h{u^2}}}{{g{b^2}}}$$
Answer :
$$n = \frac{{2h{u^2}}}{{g{b^2}}}$$
Solution :
If the ball hits the $${n^{th}}$$ step, then the horizontal distance traversed $$= nh.$$ Here, the velocity along the horizontal direction $$= u.$$ Initial velocity along the vertical direction $$= 0.$$
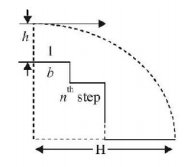
$$\eqalign{ & {\text{So}}\,nb = ut\,......\left( {\text{i}} \right) \cr & nh = 0 + \frac{1}{2}g{t^2}\,......\left( {{\text{ii}}} \right) \cr} $$
From $$t = \frac{{nb}}{v},$$ putting in eq. (ii)
$$nh = \frac{1}{2}g \times {\left( {\frac{{nb}}{u}} \right)^2}\,{\text{or}}\,n = \frac{{2h{u^2}}}{{g{b^2}}}$$
If the ball hits the $${n^{th}}$$ step, then the horizontal distance traversed $$= nh.$$ Here, the velocity along the horizontal direction $$= u.$$ Initial velocity along the vertical direction $$= 0.$$

$$\eqalign{ & {\text{So}}\,nb = ut\,......\left( {\text{i}} \right) \cr & nh = 0 + \frac{1}{2}g{t^2}\,......\left( {{\text{ii}}} \right) \cr} $$
From $$t = \frac{{nb}}{v},$$ putting in eq. (ii)
$$nh = \frac{1}{2}g \times {\left( {\frac{{nb}}{u}} \right)^2}\,{\text{or}}\,n = \frac{{2h{u^2}}}{{g{b^2}}}$$