Question
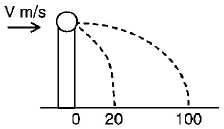
A ball of mass $$0.2kg$$ rests on a vertical post of height $$5m.$$ A bullet of mass $$0.01kg,$$ traveling with a velocity $$V m/s$$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $$20m$$ and the bullet at a distance of $$100m$$ from the foot of the post. The velocity $$V$$ of the bullet is
A ball of mass $$0.2kg$$ rests on a vertical post of height $$5m.$$ A bullet of mass $$0.01kg,$$ traveling with a velocity $$V m/s$$ in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of $$20m$$ and the bullet at a distance of $$100m$$ from the foot of the post. The velocity $$V$$ of the bullet is
A.
$$250 m/s$$
B.
$$250\sqrt 2 \,m/s$$
C.
$$400 m/s$$
D.
$$500 m/s$$
Answer :
$$500 m/s$$
Solution :
For vertical motion of bullet or ball $$u = 0,\,s = 5m,\,t = ?,\,a = 10m/{s^2}$$
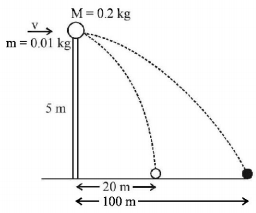
$$\eqalign{ & S = ut + \frac{1}{2}a{t^2} \Rightarrow 5 = \frac{1}{2} \times 10 \times {t^2} \cr & \Rightarrow t = 1\sec \cr} $$
For horizontal motion of ball
$${x_{ball}} = {V_{ball}}t \Rightarrow 20 = {V_{ball}} \times 1 = {V_{ball}}$$
For horizontal motion of bullet
$${x_{bullet}} = {V_{bullet}} \times t \Rightarrow 100 = {V_{bullet}} \times 1 = {V_{bullet}}$$
Applying conservation of linear momentum during collision, we get
$$\eqalign{ & mV = m{V_{bullet}} + M{V_{ball}} \cr & 0.01V = 0.01 \times 100 + 0.2 \times 20 \cr & \therefore V = \frac{5}{{0.01}} = 500m/s \cr} $$
For vertical motion of bullet or ball $$u = 0,\,s = 5m,\,t = ?,\,a = 10m/{s^2}$$

$$\eqalign{ & S = ut + \frac{1}{2}a{t^2} \Rightarrow 5 = \frac{1}{2} \times 10 \times {t^2} \cr & \Rightarrow t = 1\sec \cr} $$
For horizontal motion of ball
$${x_{ball}} = {V_{ball}}t \Rightarrow 20 = {V_{ball}} \times 1 = {V_{ball}}$$
For horizontal motion of bullet
$${x_{bullet}} = {V_{bullet}} \times t \Rightarrow 100 = {V_{bullet}} \times 1 = {V_{bullet}}$$
Applying conservation of linear momentum during collision, we get
$$\eqalign{ & mV = m{V_{bullet}} + M{V_{ball}} \cr & 0.01V = 0.01 \times 100 + 0.2 \times 20 \cr & \therefore V = \frac{5}{{0.01}} = 500m/s \cr} $$