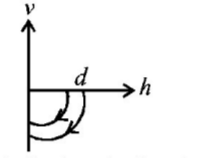
Question
A ball is thrown vertically up (taken as $$+ z$$ -axis) from the ground. The correct momentum-height ($$p-h$$ ) diagram is:
A.
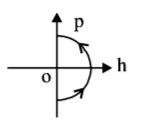

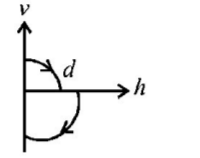
B.
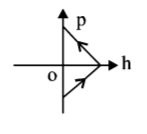

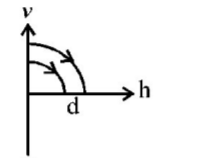
C.
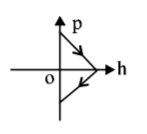

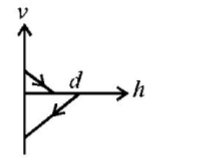
D.
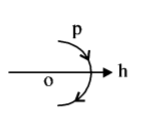

Answer :


Solution :
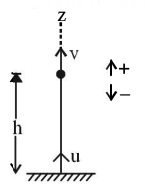
$$\eqalign{ & {v^2} = {u^2} - 2gh \cr & {\text{or}},\,v = \sqrt {{u^2} - 2gh} \cr & {\text{Momentum, }}\,p = mv{\text{ }} \cr & \therefore \,p = m\sqrt {{u^2} - 2gh} \cr} $$
Therefore graph between $$p$$ and $$h$$ cannot have straight line.
(B) and (C) are not possible.
During upward journey as $$h$$ increases, $$p$$ decreases and in downward journey as $$h$$ decreases $$p$$ increases.
Therefore (D) is the correct option.

$$\eqalign{ & {v^2} = {u^2} - 2gh \cr & {\text{or}},\,v = \sqrt {{u^2} - 2gh} \cr & {\text{Momentum, }}\,p = mv{\text{ }} \cr & \therefore \,p = m\sqrt {{u^2} - 2gh} \cr} $$
Therefore graph between $$p$$ and $$h$$ cannot have straight line.
(B) and (C) are not possible.
During upward journey as $$h$$ increases, $$p$$ decreases and in downward journey as $$h$$ decreases $$p$$ increases.
Therefore (D) is the correct option.