Question
A ball is dropped vertically from a height $$d$$ above the ground. It hits the ground and bounces up vertically to a height $$\frac{d}{2}.$$ Neglecting subsequent motion and air resistance, its velocity $$v$$ varies with the height $$h$$ above the ground as-
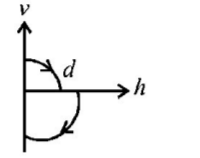
A.

B.
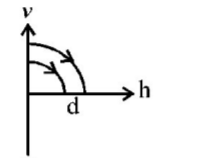

C.
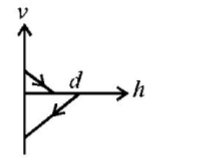

D.
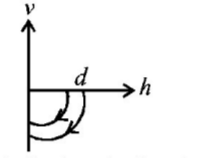

Answer :


Solution :
KEY CONCEPT
Before hitting the ground, the velocity $$v$$ is given by $$v{^2} = 2gd$$ (quadratic equation and hence parabolic path)
Downwards direction means negative velocity. After collision, the direction become positive and velocity decreases.
Further,
$$\eqalign{ & v{'^2} = 2g \times \left( {\frac{d}{2}} \right) = gd; \cr & \therefore \left( {\frac{v}{{v'}}} \right) = \sqrt 2 \,\,\,or,v = v'\sqrt 2 \cr & \Rightarrow v' = \frac{v}{{\sqrt 2 }} \cr} $$
As the direction is reversed and speed is decreased graph (A) represents these conditions correctly.
KEY CONCEPT
Before hitting the ground, the velocity $$v$$ is given by $$v{^2} = 2gd$$ (quadratic equation and hence parabolic path)
Downwards direction means negative velocity. After collision, the direction become positive and velocity decreases.
Further,
$$\eqalign{ & v{'^2} = 2g \times \left( {\frac{d}{2}} \right) = gd; \cr & \therefore \left( {\frac{v}{{v'}}} \right) = \sqrt 2 \,\,\,or,v = v'\sqrt 2 \cr & \Rightarrow v' = \frac{v}{{\sqrt 2 }} \cr} $$
As the direction is reversed and speed is decreased graph (A) represents these conditions correctly.