Question
A ball is dropped from the top of a building. The ball takes $$0.5\,s$$ to fall past the $$3m$$ length of a window some distance from the top of the building. If the velocities of the ball at the top and at the bottom of the window are $${v_T}$$ and $${v_B}$$ respectively, then (take $$g = 10\,m/{s^2}$$ )
A.
$${v_T} + {v_B} = 12\,m{s^{ - 1}}$$
B.
$${v_T} - {v_B} = 4.9\,m{s^{ - 1}}$$
C.
$${v_B}{v_T} = 1\,m{s^{ - 1}}$$
D.
$$\frac{{{v_B}}}{{{v_T}}} = 1\,m{s^{ - 1}}$$
Answer :
$${v_T} - {v_B} = 4.9\,m{s^{ - 1}}$$
Solution :
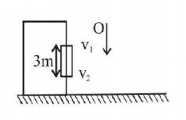
$$\eqalign{ & v_B^2 = v_T^2 + 2\left( {10} \right)\left( 3 \right) \cr & \Rightarrow v_B^2 = v_T^2 + 60\,......\left( {\text{i}} \right) \cr & {\text{Also,}}\,{v_B} = {v_T} + \left( {10} \right)\left( {0.5} \right)\,......\left( {{\text{ii}}} \right) \cr} $$
Solve eqs. (i) and (ii)
we get
$${v_T} - {v_B} = 4.9\,m{s^{ - 1}}$$

$$\eqalign{ & v_B^2 = v_T^2 + 2\left( {10} \right)\left( 3 \right) \cr & \Rightarrow v_B^2 = v_T^2 + 60\,......\left( {\text{i}} \right) \cr & {\text{Also,}}\,{v_B} = {v_T} + \left( {10} \right)\left( {0.5} \right)\,......\left( {{\text{ii}}} \right) \cr} $$
Solve eqs. (i) and (ii)
we get
$${v_T} - {v_B} = 4.9\,m{s^{ - 1}}$$