Question
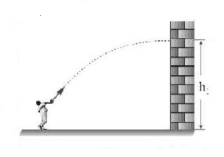
You throw a ball with a $$\vec v = \left( {3\hat i + 4\hat j} \right)m/s$$ towards a wall, where it hits at height $${h_1}.$$ Suppose that the launch velocity were, instead, $$\vec v = \left( {5\hat i + 4\hat j} \right)m/s$$ and $${h_2}$$ is height, then
You throw a ball with a $$\vec v = \left( {3\hat i + 4\hat j} \right)m/s$$ towards a wall, where it hits at height $${h_1}.$$ Suppose that the launch velocity were, instead, $$\vec v = \left( {5\hat i + 4\hat j} \right)m/s$$ and $${h_2}$$ is height, then
A.
$${h_2} = {h_1}$$
B.
$${h_2} < {h_1}$$
C.
$${h_2} > {h_1}$$
D.
$${h_2} \geqslant {h_1}$$
Answer :
$${h_2} < {h_1}$$
Solution :
$$\eqalign{ & x = 3{t_1} = 5{t_2} \Rightarrow {t_1} = \frac{x}{3}\,\,{\text{and}}\,\,{t_2} = \frac{x}{5} \cr & {\text{Now}}\,\,{h_1} = 4{t_1} - \frac{1}{2}gt_1^2 = \frac{4}{3}x - \frac{{g{x^2}}}{{18}} \cr & {\text{and}}\,\,{h_2} = 4{t_2} - \frac{1}{2}gt_2^2 = \frac{{4x}}{5} - \frac{{g{x^2}}}{{10}} \cr & {\text{Clearly,}}\,\,{h_2} < {h_1}. \cr} $$
$$\eqalign{ & x = 3{t_1} = 5{t_2} \Rightarrow {t_1} = \frac{x}{3}\,\,{\text{and}}\,\,{t_2} = \frac{x}{5} \cr & {\text{Now}}\,\,{h_1} = 4{t_1} - \frac{1}{2}gt_1^2 = \frac{4}{3}x - \frac{{g{x^2}}}{{18}} \cr & {\text{and}}\,\,{h_2} = 4{t_2} - \frac{1}{2}gt_2^2 = \frac{{4x}}{5} - \frac{{g{x^2}}}{{10}} \cr & {\text{Clearly,}}\,\,{h_2} < {h_1}. \cr} $$




