Question
Which of the following molecules has trigonal planar geometry?
A.
$$I{F_3}$$
B.
$$PC{l_3}$$
C.
$$N{H_3}$$
D.
$$B{F_3}$$
Answer :
$$B{F_3}$$
Solution :
$$I{F_3}$$ has bent-$$T$$ geometry
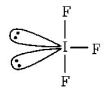
$$2lp + 3bp = s{p^3}d$$ hybridisation
$$PC{l_3}$$ has pyramidal geometry
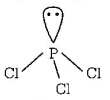
$$1lp + 3bp = s{p^3}$$ hybridisation
$$N{H_3}$$ has trigonal pyramidal geometry
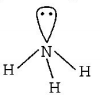
$$1lp + 3bp = s{p^3}$$ hybridisation
$$B{F_3}$$ has trigonal planar geometry
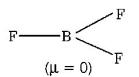
$$3bp\,\,{\text{only}} = s{p^2}$$ (hydridisation)
$$I{F_3}$$ has bent-$$T$$ geometry

$$2lp + 3bp = s{p^3}d$$ hybridisation
$$PC{l_3}$$ has pyramidal geometry

$$1lp + 3bp = s{p^3}$$ hybridisation
$$N{H_3}$$ has trigonal pyramidal geometry

$$1lp + 3bp = s{p^3}$$ hybridisation
$$B{F_3}$$ has trigonal planar geometry

$$3bp\,\,{\text{only}} = s{p^2}$$ (hydridisation)