Question
Which of the following is not the area of the region bounded by $$y = {e^x}$$ and $$x = 0$$ and $$y = e\,?$$
A.
$$e - 1$$
B.
$$\int\limits_1^e {\ln \left( {e + 1 - y} \right)dy} $$
C.
$$e - \int\limits_0^1 {{e^x}dx} $$
D.
$$\int\limits_1^e {\ln \,y\,dy} $$
Answer :
$$e - \int\limits_0^1 {{e^x}dx} $$
Solution :
Required area
$$\eqalign{ & = \int\limits_1^e {\ln \,y\,dy} \cr & = \left( {y\,\ln \,y - y} \right)_1^e \cr & = \left( {e - e} \right) - \left[ { - 1} \right] \cr & = 1 \cr} $$
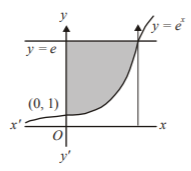
Also, $$\int\limits_1^e {\ln \,y\,dy} = \int\limits_1^e {\ln \left( {e + 1 - y} \right)dy} $$
Further, required area $$ = e \times 1 - \int\limits_0^1 {{e^x}dx} $$
Required area
$$\eqalign{ & = \int\limits_1^e {\ln \,y\,dy} \cr & = \left( {y\,\ln \,y - y} \right)_1^e \cr & = \left( {e - e} \right) - \left[ { - 1} \right] \cr & = 1 \cr} $$

Also, $$\int\limits_1^e {\ln \,y\,dy} = \int\limits_1^e {\ln \left( {e + 1 - y} \right)dy} $$
Further, required area $$ = e \times 1 - \int\limits_0^1 {{e^x}dx} $$