Question
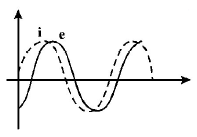
When an $$AC$$ source of emf $$e = {E_0}\sin \left( {100t} \right)$$ is connected across a circuit, the phase difference between the emf $$e$$ and the current $$i$$ in the circuit is observed to be $$\frac{\pi }{4},$$ as shown in the diagram. If the circuit consists possibly only of $$R - C$$ or $$R - L$$ or $$L - C$$ in series, find the relationship between the two elements
When an $$AC$$ source of emf $$e = {E_0}\sin \left( {100t} \right)$$ is connected across a circuit, the phase difference between the emf $$e$$ and the current $$i$$ in the circuit is observed to be $$\frac{\pi }{4},$$ as shown in the diagram. If the circuit consists possibly only of $$R - C$$ or $$R - L$$ or $$L - C$$ in series, find the relationship between the two elements
A.
$$R = 1k\Omega ,C = 10\mu F$$
B.
$$R = 1k\Omega ,C = 1\mu F$$
C.
$$R = 1k\Omega ,L = 10H$$
D.
$$R = 1k\Omega ,L = 1H$$
Answer :
$$R = 1k\Omega ,C = 10\mu F$$
Solution :
NOTE : Since current leads emf (as seen from the graph), therefore, this is an $$R - C$$ circuit.
$$\eqalign{ & \tan \phi = \frac{{{X_C} - {X_L}}}{R} \cr & {\text{Here}}\,\phi = {45^ \circ } \cr & \therefore {X_C} = R\,\,\,\,\,\,\left[ {{X_L} = 0{\text{ as there is no inductor}}} \right] \cr & \frac{1}{{\omega C}} = R \Rightarrow RC\omega = 1 \cr & \therefore RC = \frac{1}{{100}}{s^{ - 1}} \cr} $$
NOTE : Since current leads emf (as seen from the graph), therefore, this is an $$R - C$$ circuit.
$$\eqalign{ & \tan \phi = \frac{{{X_C} - {X_L}}}{R} \cr & {\text{Here}}\,\phi = {45^ \circ } \cr & \therefore {X_C} = R\,\,\,\,\,\,\left[ {{X_L} = 0{\text{ as there is no inductor}}} \right] \cr & \frac{1}{{\omega C}} = R \Rightarrow RC\omega = 1 \cr & \therefore RC = \frac{1}{{100}}{s^{ - 1}} \cr} $$