Question
What is the area of the parallelogram having diagonals $$3\hat i + \hat j - 2\hat k$$ and $$\hat i - 3\hat j + 4\hat k\,?$$
A.
$$5\sqrt 5 $$ square units
B.
$$4\sqrt 5 $$ square units
C.
$$5\sqrt 3 $$ square units
D.
$$15\sqrt 2 $$ square units
Answer :
$$5\sqrt 3 $$ square units
Solution :
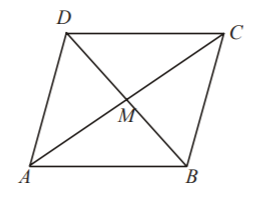
Diagonal $${d_1},\,\,\overrightarrow {AC} = 3\hat i + \hat j - 2\hat k$$
Diagonal $${d_2},\,\,\overrightarrow {BD} = \hat i - 3\hat j + 4\hat k$$
Area of parallelogram is $$\frac{1}{2}\left| {\overrightarrow {{d_1}} \times \overrightarrow {{d_2}} } \right|$$
Hence area \[ = \frac{1}{2}\left| \begin{array}{l} \hat i\,\,\,\,\,\,\,\,\,\,\hat j\,\,\,\,\,\,\,\,\,\hat k\\ 3\,\,\,\,\,\,\,\,\,\,1\,\, - 2\\ 1\,\, - 3\,\,\,\,\,\,\,\,\,4 \end{array} \right|\]
$$\eqalign{ & = \frac{1}{2}\left| {\left[ {\hat i\left( {4 - 6} \right) - \hat j\left( {12 + 2} \right) + \hat k\left( { - 9 - 1} \right)} \right]} \right| \cr & = \frac{1}{2}\left| { - 2\hat i - 14\hat j - 10\hat k} \right| \cr & = \frac{1}{2}\sqrt {4 + 196 + 100} \cr & = \frac{{10\sqrt 3 }}{2} \cr & = 5\sqrt 3 {\text{ square units}} \cr} $$
Diagonal $${d_1},\,\,\overrightarrow {AC} = 3\hat i + \hat j - 2\hat k$$
Diagonal $${d_2},\,\,\overrightarrow {BD} = \hat i - 3\hat j + 4\hat k$$

Area of parallelogram is $$\frac{1}{2}\left| {\overrightarrow {{d_1}} \times \overrightarrow {{d_2}} } \right|$$
Hence area \[ = \frac{1}{2}\left| \begin{array}{l} \hat i\,\,\,\,\,\,\,\,\,\,\hat j\,\,\,\,\,\,\,\,\,\hat k\\ 3\,\,\,\,\,\,\,\,\,\,1\,\, - 2\\ 1\,\, - 3\,\,\,\,\,\,\,\,\,4 \end{array} \right|\]
$$\eqalign{ & = \frac{1}{2}\left| {\left[ {\hat i\left( {4 - 6} \right) - \hat j\left( {12 + 2} \right) + \hat k\left( { - 9 - 1} \right)} \right]} \right| \cr & = \frac{1}{2}\left| { - 2\hat i - 14\hat j - 10\hat k} \right| \cr & = \frac{1}{2}\sqrt {4 + 196 + 100} \cr & = \frac{{10\sqrt 3 }}{2} \cr & = 5\sqrt 3 {\text{ square units}} \cr} $$