Question
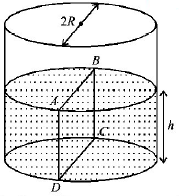
Water is filled up to a height $$h$$ in a beaker of radius $$R$$ as shown in the figure. The density of water is $$\rho ,$$ the surface tension of water is $$T$$ and the atmospheric pressure is $${P_0}.$$ Consider a vertical section $$ABCD$$ of the water column through a diameter of the beaker. The force on water on one side of this section by water on the other side of this section has magnitude
Water is filled up to a height $$h$$ in a beaker of radius $$R$$ as shown in the figure. The density of water is $$\rho ,$$ the surface tension of water is $$T$$ and the atmospheric pressure is $${P_0}.$$ Consider a vertical section $$ABCD$$ of the water column through a diameter of the beaker. The force on water on one side of this section by water on the other side of this section has magnitude
A.
$$\left| {2\,{P_0}Rh + \pi {R^2}\rho gh - 2\,RT} \right|$$
B.
$$\left| {2\,{P_0}Rh + R\rho g{h^2} - 2\,RT} \right|$$
C.
$$\left| {{P_0}\pi {R^2} + R\rho g{h^2} - 2\,RT} \right|$$
D.
$$\left| {{P_0}\pi {R^2} + R\rho g{h^2} + 2\,RT} \right|$$
Answer :
$$\left| {2\,{P_0}Rh + R\rho g{h^2} - 2\,RT} \right|$$
Solution :
The force is $$\left[ {\left( {{P_0} + \frac{{h\rho g}}{2}} \right) \times \left( {2\,R \times h} \right)} \right] - 2\,RT$$

Note : In the first part the force is created due to pressure and in the second part the force is due to surface tension $$T.$$
∴ Force $$ = 2\,{P_0}Rh + R\rho g{h^2} - 2\,RT$$
The force is $$\left[ {\left( {{P_0} + \frac{{h\rho g}}{2}} \right) \times \left( {2\,R \times h} \right)} \right] - 2\,RT$$

Note : In the first part the force is created due to pressure and in the second part the force is due to surface tension $$T.$$
∴ Force $$ = 2\,{P_0}Rh + R\rho g{h^2} - 2\,RT$$
