Question
Under which one of the following conditions does the circle $${x^2} + {y^2} + 2gx + 2fy + c = 0$$ meet the $$x$$-axis in two points on opposite sides of the origin ?
A.
$$c > 0$$
B.
$$c < 0$$
C.
$$c = 0$$
D.
$$c \leqslant 0$$
Answer :
$$c < 0$$
Solution :
For a circle to meet $$x$$-axis in two points on the opposite side of the origin its radius $$r,$$ should be more the distance of its centre from the origin.
Co-ordinate of centre of the circle $${x^2} + {y^2} + 2gx + 2fy + c = 0$$ is $$\left( { - g,\, - f} \right)\,:$$
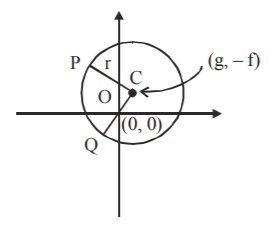
In the figure shown,
$$OQ = OP = r,$$ and distance of centre $$C,$$ from origin, $$O$$ is $$CO$$
$$\eqalign{ & r > \sqrt {OC} \,{\text{ i}}{\text{.e}}{\text{., }}r > \sqrt {{{\left( { - g} \right)}^2} + {{\left( { - f} \right)}^2}} \cr & {\text{or, }}\sqrt {{{\left( { - g} \right)}^2} + {{\left( { - f} \right)}^2} - c} > \sqrt {{{\left( { - g} \right)}^2} + {{\left( { - f} \right)}^2}} \cr & {\text{or, }}{g^2} + {f^2} - c > {g^2} + {f^2} \cr & {\text{or, }} - c > 0 \cr & {\text{or, }}c < 0 \cr} $$
For a circle to meet $$x$$-axis in two points on the opposite side of the origin its radius $$r,$$ should be more the distance of its centre from the origin.
Co-ordinate of centre of the circle $${x^2} + {y^2} + 2gx + 2fy + c = 0$$ is $$\left( { - g,\, - f} \right)\,:$$

In the figure shown,
$$OQ = OP = r,$$ and distance of centre $$C,$$ from origin, $$O$$ is $$CO$$
$$\eqalign{ & r > \sqrt {OC} \,{\text{ i}}{\text{.e}}{\text{., }}r > \sqrt {{{\left( { - g} \right)}^2} + {{\left( { - f} \right)}^2}} \cr & {\text{or, }}\sqrt {{{\left( { - g} \right)}^2} + {{\left( { - f} \right)}^2} - c} > \sqrt {{{\left( { - g} \right)}^2} + {{\left( { - f} \right)}^2}} \cr & {\text{or, }}{g^2} + {f^2} - c > {g^2} + {f^2} \cr & {\text{or, }} - c > 0 \cr & {\text{or, }}c < 0 \cr} $$