Question
Two stones of masses $$m$$ and $$2\,m$$ are whirled in horizontal circles, the heavier one in a radius $$\frac{r}{2}$$ and the lighter one in radius $$r.$$ The tangential speed of lighter stone is $$n$$ times that of the value of heavier stone when they experience same centripetal forces. The value of $$n$$ is
A.
2
B.
3
C.
4
D.
1
Answer :
2
Solution :
Given, that two stones of masses $$m$$ and $$2\,m$$ are whirled in horizontal circles, the heavier one in a radius $$\frac{r}{2}$$ and lighter one in radius $$r$$ as shown in figure.
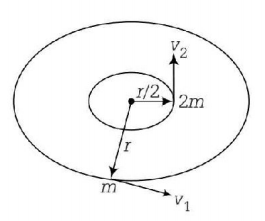
As, lighter stone is $$n$$ times that of the value of heavier stone when they experience same centripetal forces, we get
$$\eqalign{ & {\left( {{F_c}} \right)_{{\text{heavier}}}} = {\left( {{F_c}} \right)_{{\text{lighter}}}} \cr & \Rightarrow \frac{{2m{{\left( v \right)}^2}}}{{\left( {\frac{r}{2}} \right)}} = \frac{{m{{\left( {nv} \right)}^2}}}{r} \cr & \Rightarrow {n^2} = 4 \Rightarrow n = 2 \cr} $$
Given, that two stones of masses $$m$$ and $$2\,m$$ are whirled in horizontal circles, the heavier one in a radius $$\frac{r}{2}$$ and lighter one in radius $$r$$ as shown in figure.

As, lighter stone is $$n$$ times that of the value of heavier stone when they experience same centripetal forces, we get
$$\eqalign{ & {\left( {{F_c}} \right)_{{\text{heavier}}}} = {\left( {{F_c}} \right)_{{\text{lighter}}}} \cr & \Rightarrow \frac{{2m{{\left( v \right)}^2}}}{{\left( {\frac{r}{2}} \right)}} = \frac{{m{{\left( {nv} \right)}^2}}}{r} \cr & \Rightarrow {n^2} = 4 \Rightarrow n = 2 \cr} $$




