Question
Two spheres $$A$$ and $$B$$ of masses $${m_1}$$ and $${m_2}$$ respectively collide. $$A$$ is at rest initially and $$B$$ is moving with velocity $$v$$ along $$x$$-axis. After collision, $$B$$ has a velocity $$\frac{v}{2}$$ in a direction perpendicular to the original direction. The mass $$A$$ moves after collision in the direction
A.
same as that of $$B$$
B.
opposite to that of $$B$$
C.
$$\theta = {\tan ^{ - 1}}\left( {\frac{1}{2}} \right)$$ to the $$x$$-axis
D.
$$\theta = {\tan ^{ - 1}}\left( {\frac{{ - 1}}{2}} \right)$$ to the $$x$$-axis
Answer :
$$\theta = {\tan ^{ - 1}}\left( {\frac{1}{2}} \right)$$ to the $$x$$-axis
Solution :
Here, $${p_i} = {m_2}vi + {m_1} \times 0$$
$${p_f} = {m_2}\frac{v}{2}\hat j + {m_1} \times {v_1}$$
Law of conservation of momentum
$$\eqalign{ & {p_i} = {p_f} \cr & {m_2}v\hat i = {m_2}\frac{v}{2}\hat j + {m_1} \times {v_1} \cr & {v_1} = \frac{{{m_2}}}{{{m_1}}}v\hat i + \frac{{{m_2}}}{{{m_1}}}\frac{v}{2}\hat j \cr} $$
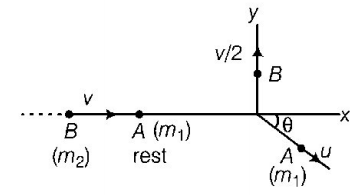
From this equation, we can find
$$\tan \theta = \frac{y}{x} = \frac{1}{2},\,\theta = {\tan ^{ - 1}}\left( {\frac{1}{2}} \right)$$ to the $$x$$-axis.
Here, $${p_i} = {m_2}vi + {m_1} \times 0$$
$${p_f} = {m_2}\frac{v}{2}\hat j + {m_1} \times {v_1}$$
Law of conservation of momentum
$$\eqalign{ & {p_i} = {p_f} \cr & {m_2}v\hat i = {m_2}\frac{v}{2}\hat j + {m_1} \times {v_1} \cr & {v_1} = \frac{{{m_2}}}{{{m_1}}}v\hat i + \frac{{{m_2}}}{{{m_1}}}\frac{v}{2}\hat j \cr} $$

From this equation, we can find
$$\tan \theta = \frac{y}{x} = \frac{1}{2},\,\theta = {\tan ^{ - 1}}\left( {\frac{1}{2}} \right)$$ to the $$x$$-axis.
