Question
Two sources of equal emf are connected to an external resistance $$R.$$ The internal resistance of the two sources are $${R_1}$$ and $${R_2}\left( {{R_1} > {R_1}} \right).$$ If the potential difference across the source having internal resistance $${R_2}$$ is zero, then
A.
$$R = {R_2} - {R_1}$$
B.
$$R = \frac{{{R_2} \times \left( {{R_1} + {R_2}} \right)}}{{\left( {{R_2} - {R_1}} \right)}}$$
C.
$$R = \frac{{{R_1}{R_2}}}{{\left( {{R_2} - {R_1}} \right)}}$$
D.
$$R = \frac{{{R_1}{R_2}}}{{\left( {{R_1} - {R_2}} \right)}}$$
Answer :
$$R = {R_2} - {R_1}$$
Solution :
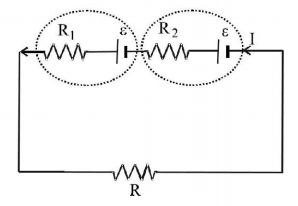
$$I = \frac{{2\varepsilon }}{{R + {R_1} + {R_2}}}$$
Potential difference across second cell $$ = V = \varepsilon - I{R_2} = 0$$
$$\eqalign{ & \varepsilon - \frac{{2\varepsilon }}{{R + {R_1} + {R_2}}}.{R_2} = 0 \cr & R + {R_1} + {R_2} - 2{R_2} = 0 \cr & R + {R_1} - {R_2} = 0\,\,\,\,\,\,\,\,\,\,\,\,\therefore R = {R_2} - {R_1} \cr} $$

$$I = \frac{{2\varepsilon }}{{R + {R_1} + {R_2}}}$$
Potential difference across second cell $$ = V = \varepsilon - I{R_2} = 0$$
$$\eqalign{ & \varepsilon - \frac{{2\varepsilon }}{{R + {R_1} + {R_2}}}.{R_2} = 0 \cr & R + {R_1} + {R_2} - 2{R_2} = 0 \cr & R + {R_1} - {R_2} = 0\,\,\,\,\,\,\,\,\,\,\,\,\therefore R = {R_2} - {R_1} \cr} $$
