Question
Two short bar magnets of length $$1 cm$$ each have magnetic moments $$1.20\,A{m^2}$$ and $$1.00\,A{m^2}$$ respectively. They are placed on a horizontal table parallel to each other with their $$N$$ poles pointing towards the South. They have a common magnetic equator and are separated by a distance of $$20.0 cm.$$ The value of the resultand horizontal magnetic induction at the mid-point $$O$$ of the line joining their centres is close to (Horizontal component of earth.s magnetic induction is $$3.6 \times 10.5\,Wb/{m^2}$$ )
A.
$$3.6 \times 10.5\,Wb/{m^2}$$
B.
$$2.56 \times 10.4\,Wb/{m^2}$$
C.
$$3.50 \times 10.4\,Wb/{m^2}$$
D.
$$5.80 \times 10.4\,Wb/{m^2}$$
Answer :
$$2.56 \times 10.4\,Wb/{m^2}$$
Solution :
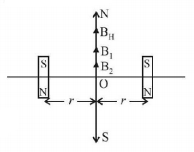
Given : $${M_1} = 1.20A{m^2}\,{\text{and}}\,{M_2} = 1.00A{m^2}$$
$$\eqalign{ & r = \frac{{20}}{2}\;cm = 0.1\;m \cr & {B_{{\text{net}}}} = {B_1} + {B_2} + {B_H} \cr & {B_{{\text{net}}}} = \frac{{{\mu _0}}}{{4\pi }}\frac{{\left( {{M_1} + {M_2}} \right)}}{{{r^3}}} + {B_H} \cr & = \frac{{{{10}^{ - 7}}\left( {1.2 + 1} \right)}}{{{{\left( {0.1} \right)}^3}}} + 3.6 \times {10^{ - 5}} = 2.56 \times {10^{ - 4}}wb/{m^2} \cr} $$

Given : $${M_1} = 1.20A{m^2}\,{\text{and}}\,{M_2} = 1.00A{m^2}$$
$$\eqalign{ & r = \frac{{20}}{2}\;cm = 0.1\;m \cr & {B_{{\text{net}}}} = {B_1} + {B_2} + {B_H} \cr & {B_{{\text{net}}}} = \frac{{{\mu _0}}}{{4\pi }}\frac{{\left( {{M_1} + {M_2}} \right)}}{{{r^3}}} + {B_H} \cr & = \frac{{{{10}^{ - 7}}\left( {1.2 + 1} \right)}}{{{{\left( {0.1} \right)}^3}}} + 3.6 \times {10^{ - 5}} = 2.56 \times {10^{ - 4}}wb/{m^2} \cr} $$