Question
Two point source $${S_1}$$ and $${S_2}$$ are $$24\,cm$$ apart. Where should a convex lens of focal length $$9\,cm$$ be placed in between them so that the images of both sources are formed at the same place?
A.
$$6\,cm$$ from $${S_1}$$
B.
$$15\,cm$$ from $${S_1}$$
C.
$$10\,cm$$ from $${S_1}$$
D.
$$12\,cm$$ from $${S_1}$$
Answer :
$$6\,cm$$ from $${S_1}$$
Solution :
In this case, one of the image will be real and the other virtual. Let us assume that image of $${S_1}$$ is real and that of $${S_2}$$ is virtual.
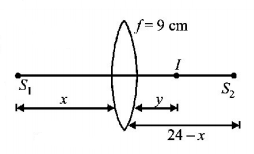
Applying $$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$
For $${S_1}:\frac{1}{y} + \frac{1}{x} = \frac{1}{9}\,......\left( {\text{i}} \right)$$
For $${S_2}:\frac{1}{y} + \frac{1}{{24 - x}} = \frac{1}{9}\,......\left( {{\text{ii}}} \right)$$
Solving eqs. (i) and (ii),
we get $$x = 6\,cm$$
In this case, one of the image will be real and the other virtual. Let us assume that image of $${S_1}$$ is real and that of $${S_2}$$ is virtual.

Applying $$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$$
For $${S_1}:\frac{1}{y} + \frac{1}{x} = \frac{1}{9}\,......\left( {\text{i}} \right)$$
For $${S_2}:\frac{1}{y} + \frac{1}{{24 - x}} = \frac{1}{9}\,......\left( {{\text{ii}}} \right)$$
Solving eqs. (i) and (ii),
we get $$x = 6\,cm$$

