Question
Two particles start simultaneously from the same point and move along two straight lines, one with uniform velocity $$\overrightarrow u $$ and the other from rest with uniform acceleration $$\overrightarrow f .$$ Let $$\alpha $$ be the angle between their directions of motion. The relative velocity of the second particle w.r.t. the first is least after a time :
A.
$$\frac{{u\,\cos \,\alpha }}{f}$$
B.
$$\frac{{u\,\sin \,\alpha }}{f}$$
C.
$$\frac{{f\,\cos \,\alpha }}{u}$$
D.
$${u\,\sin \,\alpha }$$
Answer :
$$\frac{{u\,\cos \,\alpha }}{f}$$
Solution :
We can consider the two velocities as $$\overrightarrow {{v_1}} = u\hat i{\text{ and }}\overrightarrow {{v_2}} = \left( {ft\,\cos \,\alpha } \right)\hat i + \left( {ft\,\sin \,\alpha } \right)\hat j$$
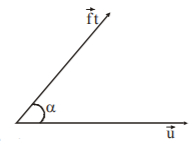
$$\therefore $$ Relative velocity of second with respect to first
$$\eqalign{ & \overrightarrow v = \overrightarrow {{v_2}} - \overrightarrow {{v_1}} = \left( {ft\,\cos \,\alpha - u} \right)\hat i + \left( {ft\,\sin \,\alpha } \right)\hat j \cr & \Rightarrow {\left| {\overrightarrow v } \right|^2} = {\left( {ft\,\cos \,\alpha - u} \right)^2} + {\left( {ft\,\sin \,\alpha } \right)^2} \cr & \Rightarrow {\left| {\overrightarrow v } \right|^2} = {f^2}{t^2} + {u^2} - 2uft\,\cos \,\alpha \cr} $$
For $$\left| {\overrightarrow v } \right|$$ to be min we should have
$$\eqalign{ & \frac{{d{{\left| v \right|}^2}}}{{dt}} = 0 \cr & \Rightarrow 2{f^2}t - 2uf\,\cos \,\alpha = 0 \cr & \Rightarrow t = \frac{{u\,\cos \,\alpha }}{f} \cr} $$
Also, $$\frac{{{d^2}{{\left| v \right|}^2}}}{{d{t^2}}} = 2{f^2} = + ve$$
$$\therefore \,{\left| v \right|^2}$$ and hence $$\left| v \right|$$ is least at the time $$\frac{{u\,\cos \,\alpha }}{f}$$
We can consider the two velocities as $$\overrightarrow {{v_1}} = u\hat i{\text{ and }}\overrightarrow {{v_2}} = \left( {ft\,\cos \,\alpha } \right)\hat i + \left( {ft\,\sin \,\alpha } \right)\hat j$$

$$\therefore $$ Relative velocity of second with respect to first
$$\eqalign{ & \overrightarrow v = \overrightarrow {{v_2}} - \overrightarrow {{v_1}} = \left( {ft\,\cos \,\alpha - u} \right)\hat i + \left( {ft\,\sin \,\alpha } \right)\hat j \cr & \Rightarrow {\left| {\overrightarrow v } \right|^2} = {\left( {ft\,\cos \,\alpha - u} \right)^2} + {\left( {ft\,\sin \,\alpha } \right)^2} \cr & \Rightarrow {\left| {\overrightarrow v } \right|^2} = {f^2}{t^2} + {u^2} - 2uft\,\cos \,\alpha \cr} $$
For $$\left| {\overrightarrow v } \right|$$ to be min we should have
$$\eqalign{ & \frac{{d{{\left| v \right|}^2}}}{{dt}} = 0 \cr & \Rightarrow 2{f^2}t - 2uf\,\cos \,\alpha = 0 \cr & \Rightarrow t = \frac{{u\,\cos \,\alpha }}{f} \cr} $$
Also, $$\frac{{{d^2}{{\left| v \right|}^2}}}{{d{t^2}}} = 2{f^2} = + ve$$
$$\therefore \,{\left| v \right|^2}$$ and hence $$\left| v \right|$$ is least at the time $$\frac{{u\,\cos \,\alpha }}{f}$$