Question
Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes, They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is
A.
0
B.
$$\frac{{2\pi }}{3}$$
C.
$$\pi $$
D.
$$\frac{{\pi }}{6}$$
Answer :
$$\frac{{2\pi }}{3}$$
Solution :
Equation of $$S.H.M.$$ is given by
$$x = A\sin \left( {\omega t + \delta } \right)$$
$$\left( {\omega t + \delta } \right)$$ is called phase.
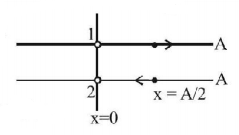
$$\eqalign{ & {\text{When}}\,\,x = \frac{A}{2},\,{\text{then}}\,\sin \left( {\omega t + \delta } \right) = \frac{1}{2} \cr & \Rightarrow \omega t + \delta = \frac{\pi }{6} \cr & {\text{or}}\,\,{\phi _1} = \frac{\pi }{6} \cr & {\text{For second particle,}} \cr & {\phi _2} = \pi - \frac{\pi }{6} = \frac{{5\pi }}{6} \cr & \therefore \phi = {\phi _2} - {\phi _1} = \frac{{4\pi }}{6} = \frac{{2\pi }}{3} \cr} $$
Equation of $$S.H.M.$$ is given by
$$x = A\sin \left( {\omega t + \delta } \right)$$
$$\left( {\omega t + \delta } \right)$$ is called phase.

$$\eqalign{ & {\text{When}}\,\,x = \frac{A}{2},\,{\text{then}}\,\sin \left( {\omega t + \delta } \right) = \frac{1}{2} \cr & \Rightarrow \omega t + \delta = \frac{\pi }{6} \cr & {\text{or}}\,\,{\phi _1} = \frac{\pi }{6} \cr & {\text{For second particle,}} \cr & {\phi _2} = \pi - \frac{\pi }{6} = \frac{{5\pi }}{6} \cr & \therefore \phi = {\phi _2} - {\phi _1} = \frac{{4\pi }}{6} = \frac{{2\pi }}{3} \cr} $$