Question
Two long parallel wires are at a distance of $$1\,m.$$ Both of them carry $$1A$$ of current. The force of attraction per unit length between the two wires is
A.
$$2 \times {10^{ - 7}}N/m$$
B.
$$2 \times {10^{ - 8}}N/m$$
C.
$$5 \times {10^{ - 8}}N/m$$
D.
$${10^{ - 7}}N/m$$
Answer :
$$2 \times {10^{ - 7}}N/m$$
Solution :
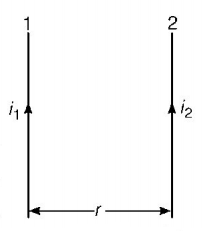
Magnetic force between parallel wires per unit length is given by $$\frac{F}{l} = \frac{{{\mu _0}}}{{2\pi }} \times \frac{{{i_1}{i_2}}}{r}$$
where, $${{i_1}}$$ and $${{i_2}}$$ are the currents in wires 1 and 2 respectively and $$r$$ is the distance between them.
Since, it is given that between two wires there is a force of attraction, so, the direction of currents in both will be the same.
$$\eqalign{ & {\text{Given,}}\,{i_1} = {i_2} = 1A,r = 1\,m, \cr & {\mu _0} = 4\pi \times {10^{ - 7}}T{\text{ - }}m/A \cr & \therefore \frac{F}{l} = \frac{{4\pi \times {{10}^{ - 7}}}}{{2\pi }} \times \frac{{1 \times 1}}{1} \cr & = 2 \times {10^{ - 7}}N/m \cr} $$
NOTE
When current is in same direction in both the wires there will be attraction and if current in opposite direction there is repulsion.

Magnetic force between parallel wires per unit length is given by $$\frac{F}{l} = \frac{{{\mu _0}}}{{2\pi }} \times \frac{{{i_1}{i_2}}}{r}$$
where, $${{i_1}}$$ and $${{i_2}}$$ are the currents in wires 1 and 2 respectively and $$r$$ is the distance between them.
Since, it is given that between two wires there is a force of attraction, so, the direction of currents in both will be the same.
$$\eqalign{ & {\text{Given,}}\,{i_1} = {i_2} = 1A,r = 1\,m, \cr & {\mu _0} = 4\pi \times {10^{ - 7}}T{\text{ - }}m/A \cr & \therefore \frac{F}{l} = \frac{{4\pi \times {{10}^{ - 7}}}}{{2\pi }} \times \frac{{1 \times 1}}{1} \cr & = 2 \times {10^{ - 7}}N/m \cr} $$
NOTE
When current is in same direction in both the wires there will be attraction and if current in opposite direction there is repulsion.