Question
Two lines $$2x-3y=1$$ and $$x+2y+3=0$$ divide the $$x$$-$$y$$ plane in four compartments which are named as shown in the figure. Consider the locations of the points $$\left( {2,\, - 1} \right)\left( {3,\,2} \right)$$ and $$\left( { - 1,\, - 2} \right).$$ We get
Two lines $$2x-3y=1$$ and $$x+2y+3=0$$ divide the $$x$$-$$y$$ plane in four compartments which are named as shown in the figure. Consider the locations of the points $$\left( {2,\, - 1} \right)\left( {3,\,2} \right)$$ and $$\left( { - 1,\, - 2} \right).$$ We get
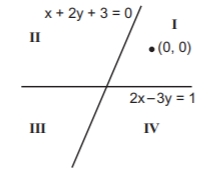
A.
$$\left( {2,\, - 1} \right) \in \,{\text{IV}}$$
B.
$$\left( {3,\,2} \right)\, \in \,{\text{III}}$$
C.
$$\left( { - 1,\, - 2} \right)\, \in \,{\text{II}}$$
D.
none of these
Answer :
$$\left( {2,\, - 1} \right) \in \,{\text{IV}}$$
Solution :
Consider the first line
$$\eqalign{ & 2x - 3y = 1 \cr & \frac{x}{{\frac{1}{2}}} - \frac{y}{{\frac{1}{3}}} = 1 \cr} $$
Hence the intercepts are $$\frac{1}{2}$$ and $$\left( { - \frac{1}{3}} \right)......\left( {\text{i}} \right)$$
Similarly for the second line $$\frac{x}{{ - 3}} + \frac{y}{{\frac{{ - 3}}{2}}} = 1$$
Hence it has intercepts $$-3$$ and $$-1.5$$
Now both the lines intersect at $$\left( { - 1,\, - 1} \right)$$
This will be our origin.
Hence
Now consider the point $$\left( {2,\, - 1} \right)$$
Substituting the point in $$2x - 3y - 1 = 0$$
We get
$$8 > 0......\left( {\text{i}} \right)$$
Substituting it in $$x + 2y + 3 = 0$$
$$3 > 0......\left( {{\text{ii}}} \right)$$
Clearly from i and ii, it will lie in the new iv quadrant. Similarly applying the above steps for the point $$\left( {3,\,2} \right)$$ and $$\left( { - 1,\,2} \right)$$ we get that the point $$\left( {3,\,2} \right)$$ lies in the new first quadrant while the point $$\left( { - 1,\, - 2} \right)$$ lies in the new IIIrd quadrant.
Consider the first line
$$\eqalign{ & 2x - 3y = 1 \cr & \frac{x}{{\frac{1}{2}}} - \frac{y}{{\frac{1}{3}}} = 1 \cr} $$
Hence the intercepts are $$\frac{1}{2}$$ and $$\left( { - \frac{1}{3}} \right)......\left( {\text{i}} \right)$$
Similarly for the second line $$\frac{x}{{ - 3}} + \frac{y}{{\frac{{ - 3}}{2}}} = 1$$
Hence it has intercepts $$-3$$ and $$-1.5$$
Now both the lines intersect at $$\left( { - 1,\, - 1} \right)$$
This will be our origin.
Hence
Now consider the point $$\left( {2,\, - 1} \right)$$
Substituting the point in $$2x - 3y - 1 = 0$$
We get
$$8 > 0......\left( {\text{i}} \right)$$
Substituting it in $$x + 2y + 3 = 0$$
$$3 > 0......\left( {{\text{ii}}} \right)$$
Clearly from i and ii, it will lie in the new iv quadrant. Similarly applying the above steps for the point $$\left( {3,\,2} \right)$$ and $$\left( { - 1,\,2} \right)$$ we get that the point $$\left( {3,\,2} \right)$$ lies in the new first quadrant while the point $$\left( { - 1,\, - 2} \right)$$ lies in the new IIIrd quadrant.