Question
Two identical thin rings each of radius $$R$$ meters are coaxially placed at a distance $$R$$ meters apart. If $${Q_1}$$ coulomb and $${Q_2}$$ coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge $$q$$ from the centre of one ring to that of other is
A.
zero
B.
$$\frac{{q\left( {{Q_1} - {Q_2}} \right)\left( {\sqrt 2 - 1} \right)}}{{\sqrt 2 .4\pi {\varepsilon _0}R}}$$
C.
$$\frac{{q\sqrt 2 \left( {{Q_1} + {Q_2}} \right)}}{{4\pi {\varepsilon _0}R}}$$
D.
$$\frac{{q\left( {{Q_1} + {Q_2}} \right)\left( {\sqrt 2 + 1} \right)}}{{\sqrt 2 .4\pi {\varepsilon _0}R}}$$
Answer :
$$\frac{{q\left( {{Q_1} - {Q_2}} \right)\left( {\sqrt 2 - 1} \right)}}{{\sqrt 2 .4\pi {\varepsilon _0}R}}$$
Solution :
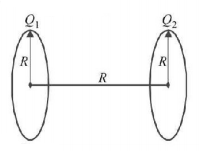
$$\eqalign{ & {\text{Work}}\,{\text{done}}\,\,{W_{21}} = \left( {{V_1} - {V_2}} \right)q \cr & {V_1} = \frac{1}{{4\pi { \in _0}}}\left[ {\frac{{{Q_1}}}{R} + \frac{{{Q_2}}}{{\sqrt 2 R}}} \right] \cr & {\text{and}}\,\,{V_2} = \frac{1}{{4\pi { \in _0}}}\left[ {\frac{{{Q_2}}}{R} + \frac{{{Q_1}}}{{\sqrt 2 R}}} \right] \cr & {\text{Thus,}}\,{W_{21}} = \frac{{q\left( {{Q_1} - {Q_2}} \right)\left( {\sqrt 2 - 1} \right)}}{{\sqrt 2 .4\pi { \in _0}R}}. \cr} $$

$$\eqalign{ & {\text{Work}}\,{\text{done}}\,\,{W_{21}} = \left( {{V_1} - {V_2}} \right)q \cr & {V_1} = \frac{1}{{4\pi { \in _0}}}\left[ {\frac{{{Q_1}}}{R} + \frac{{{Q_2}}}{{\sqrt 2 R}}} \right] \cr & {\text{and}}\,\,{V_2} = \frac{1}{{4\pi { \in _0}}}\left[ {\frac{{{Q_2}}}{R} + \frac{{{Q_1}}}{{\sqrt 2 R}}} \right] \cr & {\text{Thus,}}\,{W_{21}} = \frac{{q\left( {{Q_1} - {Q_2}} \right)\left( {\sqrt 2 - 1} \right)}}{{\sqrt 2 .4\pi { \in _0}R}}. \cr} $$