Question
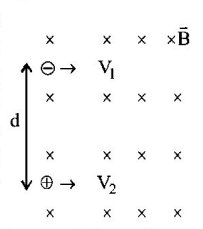
Two identical particles having the same mass $$m$$ and charges $$+q$$ and $$-q$$ separated by a distance $$d$$ enter a uniform magnetic field $$B$$ directed perpendicular to paper inwards with in speeds $${v_1}$$ and $${v_2}$$ as shown in Fig. The particles will not collide if
Two identical particles having the same mass $$m$$ and charges $$+q$$ and $$-q$$ separated by a distance $$d$$ enter a uniform magnetic field $$B$$ directed perpendicular to paper inwards with in speeds $${v_1}$$ and $${v_2}$$ as shown in Fig. The particles will not collide if
A.
$$d > \frac{m}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
B.
$$d < \frac{m}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
C.
$$d > \frac{{2m}}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
D.
$${v_1} = {v_2}$$
Answer :
$$d > \frac{{2m}}{{Bq}}\left( {{v_1} + {v_2}} \right)$$
Solution :
The particle will not collide if
$$\eqalign{ & d > 2\left( {{r_1} + {r_2}} \right) \cr & {\text{or}}\,\,d > 2\left( {\frac{{m{v_1}}}{{Bq}} + \frac{{m{v_2}}}{{Bq}}} \right)\,\,{\text{or}}\,\,d > \frac{{2m}}{{Bq}}\left( {{v_1} + {v_2}} \right) \cr} $$
The particle will not collide if
$$\eqalign{ & d > 2\left( {{r_1} + {r_2}} \right) \cr & {\text{or}}\,\,d > 2\left( {\frac{{m{v_1}}}{{Bq}} + \frac{{m{v_2}}}{{Bq}}} \right)\,\,{\text{or}}\,\,d > \frac{{2m}}{{Bq}}\left( {{v_1} + {v_2}} \right) \cr} $$