Question
Two identical particles are projected horizontally in opposite directions with a speed of $$5\,m{s^{ - 1}}$$ each from the top of a tall tower as shown. Assuming $$g = 10\,m{s^{ - 2}},$$ the distance between them at the moment when their velocity vectors become mutually perpendicular is
Two identical particles are projected horizontally in opposite directions with a speed of $$5\,m{s^{ - 1}}$$ each from the top of a tall tower as shown. Assuming $$g = 10\,m{s^{ - 2}},$$ the distance between them at the moment when their velocity vectors become mutually perpendicular is

A.
$$2.5\,m$$
B.
$$5\,m$$
C.
$$10\,m$$
D.
$$20\,m$$
Answer :
$$5\,m$$
Solution :
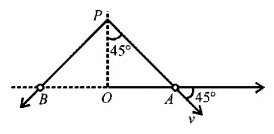
At a time $$t$$ when velocity vector become mutually perpendicular
$$\eqalign{ & v\cos {45^ \circ } = 5\,{\text{horizontal component}} \cr & v = \frac{5}{{\cos {{45}^ \circ }}} = 5\sqrt 2 \,m/s \cr} $$
Vertically,
$$\eqalign{ & v\sin {45^ \circ } = gt \cr & \Rightarrow t = \frac{{v\sin {{45}^ \circ }}}{g} = \frac{{5\sqrt 2 \times \frac{1}{{\sqrt 2 }}}}{{10}} = \frac{1}{2} \cr & {\text{so,}}\,\,OA = OB = v\cos {45^ \circ } \times t = 5 \times \frac{1}{2} = 2.5 \cr & \Rightarrow AB = 2.5 \times 2 = 5\,m \cr} $$

At a time $$t$$ when velocity vector become mutually perpendicular
$$\eqalign{ & v\cos {45^ \circ } = 5\,{\text{horizontal component}} \cr & v = \frac{5}{{\cos {{45}^ \circ }}} = 5\sqrt 2 \,m/s \cr} $$
Vertically,
$$\eqalign{ & v\sin {45^ \circ } = gt \cr & \Rightarrow t = \frac{{v\sin {{45}^ \circ }}}{g} = \frac{{5\sqrt 2 \times \frac{1}{{\sqrt 2 }}}}{{10}} = \frac{1}{2} \cr & {\text{so,}}\,\,OA = OB = v\cos {45^ \circ } \times t = 5 \times \frac{1}{2} = 2.5 \cr & \Rightarrow AB = 2.5 \times 2 = 5\,m \cr} $$




