Question
Two identical coherent sources are placed on a diameter of a circle of radius $$R$$ at separation $$x\left( { < < R} \right)$$ symmetrical about the center of the circle. The sources emit identical wavelength $$\lambda $$ each. The number of points on the circle of maximum intersity is $$\left( {x = 5\lambda } \right)$$
A.
20
B.
22
C.
24
D.
26
Answer :
20
Solution :
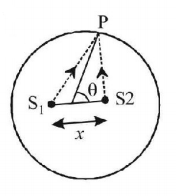
Path difference at $$P$$ is
$$\Delta x = 2\left( {\frac{x}{2}\cos \theta } \right) = x\cos \theta $$
For intensity to be maximum,
$$\eqalign{ & \Delta x = n\lambda \,\,\left( {n = 0,1,2,3,......} \right) \cr & {\text{or}}\,\,x\cos \theta = n\lambda \cr & {\text{or}}\,\,\cos \theta = \frac{{n\lambda }}{x} \geqslant 1 \cr & \therefore n \geqslant \frac{x}{\lambda } \cr & {\text{Subsituting }}x = 51,\,{\text{we get}} \cr & n \geqslant 5\,{\text{or}}\,\,n = 1,2,3,4,5,....... \cr} $$
Therefore in all four quadrants there can be 20 maxima. There are more maxima at $$\theta = {0^ \circ }\,{\text{and}}\,\theta = {180^ \circ }.$$ But $$n = 5$$ corresponds to $$\theta = {90^ \circ }\,{\text{and}}\,\theta = {270^ \circ }$$ which are coming only twice while we have multiplies it four times. Therefore, total number of maxima are still 20, i.e., $$n = 1$$ to 4 in four quadrants (total 16) plus more at $$\theta = {0^ \circ },{90^ \circ },{180^ \circ }\,{\text{and}}\,{270^ \circ }.$$

Path difference at $$P$$ is
$$\Delta x = 2\left( {\frac{x}{2}\cos \theta } \right) = x\cos \theta $$
For intensity to be maximum,
$$\eqalign{ & \Delta x = n\lambda \,\,\left( {n = 0,1,2,3,......} \right) \cr & {\text{or}}\,\,x\cos \theta = n\lambda \cr & {\text{or}}\,\,\cos \theta = \frac{{n\lambda }}{x} \geqslant 1 \cr & \therefore n \geqslant \frac{x}{\lambda } \cr & {\text{Subsituting }}x = 51,\,{\text{we get}} \cr & n \geqslant 5\,{\text{or}}\,\,n = 1,2,3,4,5,....... \cr} $$
Therefore in all four quadrants there can be 20 maxima. There are more maxima at $$\theta = {0^ \circ }\,{\text{and}}\,\theta = {180^ \circ }.$$ But $$n = 5$$ corresponds to $$\theta = {90^ \circ }\,{\text{and}}\,\theta = {270^ \circ }$$ which are coming only twice while we have multiplies it four times. Therefore, total number of maxima are still 20, i.e., $$n = 1$$ to 4 in four quadrants (total 16) plus more at $$\theta = {0^ \circ },{90^ \circ },{180^ \circ }\,{\text{and}}\,{270^ \circ }.$$