Question
Two identical charged spheres suspended from a common point by two massless strings of lengths $$l,$$ are initially at a distance $$d\left( {d < < l} \right)$$ apart because of their mutual repulsion. The charges begin to leak from both the spheres at a constant rate. As a result, the spheres approach each other with a velocity $$v.$$ Then, $$v$$ varies as a function of the distance $$x$$ between the sphere, as
A.
$$v \propto x$$
B.
$$v \propto {x^{ - \frac{1}{2}}}$$
C.
$$v \propto {x^{ - 1}}$$
D.
$$v \propto {x^{\frac{1}{2}}}$$
Answer :
$$v \propto {x^{ - \frac{1}{2}}}$$
Solution :
According to question, two identical charged spheres suspended from a common point by two massless strings of length $$L.$$
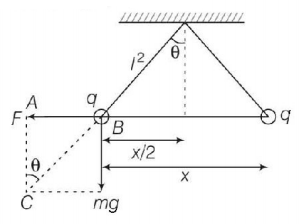
$$\because {\text{In,}}\,\,\Delta ABC\,\tan \theta = \frac{F}{{mg}}\,\,{\text{or}}\,\theta \frac{F}{{mg}} = \tan \theta \,......\left( {\text{i}} \right)$$
Since, the charges begins to leak from both the spheres at a constant rate. As a result, the spheres approach each other with velocity $$v.$$
Therefore, Eq. (i) can be rewritten as
$$\eqalign{ & \frac{{K{q^2}}}{{{x^2}mg}} = \frac{{\frac{x}{2}}}{{\sqrt {{l^2} - \frac{{{x^2}}}{4}} }} \cr & \Rightarrow \frac{{K{q^2}}}{{{x^2}mg}} = \frac{x}{{2l}}\,\,{\text{or}}\,\,{q^2} \propto {x^3} \cr & \Rightarrow q \propto {x^{\frac{3}{2}}} \cr & \Rightarrow \frac{{dq}}{{dt}} \propto \frac{{d\left( {{x^{\frac{3}{2}}}} \right)}}{{dx}} \cdot \frac{{dx}}{{dt}} \cr & \Rightarrow \frac{{dq}}{{dt}} \propto {x^{\frac{1}{2}}} \cdot v \cr & \Rightarrow v \propto \frac{1}{{{x^{\frac{1}{2}}}}}\,\,{\text{or}}\,\,v \propto {x^{ - \frac{1}{2}}} \cr} $$
According to question, two identical charged spheres suspended from a common point by two massless strings of length $$L.$$

$$\because {\text{In,}}\,\,\Delta ABC\,\tan \theta = \frac{F}{{mg}}\,\,{\text{or}}\,\theta \frac{F}{{mg}} = \tan \theta \,......\left( {\text{i}} \right)$$
Since, the charges begins to leak from both the spheres at a constant rate. As a result, the spheres approach each other with velocity $$v.$$
Therefore, Eq. (i) can be rewritten as
$$\eqalign{ & \frac{{K{q^2}}}{{{x^2}mg}} = \frac{{\frac{x}{2}}}{{\sqrt {{l^2} - \frac{{{x^2}}}{4}} }} \cr & \Rightarrow \frac{{K{q^2}}}{{{x^2}mg}} = \frac{x}{{2l}}\,\,{\text{or}}\,\,{q^2} \propto {x^3} \cr & \Rightarrow q \propto {x^{\frac{3}{2}}} \cr & \Rightarrow \frac{{dq}}{{dt}} \propto \frac{{d\left( {{x^{\frac{3}{2}}}} \right)}}{{dx}} \cdot \frac{{dx}}{{dt}} \cr & \Rightarrow \frac{{dq}}{{dt}} \propto {x^{\frac{1}{2}}} \cdot v \cr & \Rightarrow v \propto \frac{1}{{{x^{\frac{1}{2}}}}}\,\,{\text{or}}\,\,v \propto {x^{ - \frac{1}{2}}} \cr} $$
